Problem:
For a real number , let denote the greatest integer less than or equal to . Let denote the region in the coordinate plane consisting of points such that
The region is completely contained in a disk of radius (a disk is the union of a circle and its interior). The minimum value of can be written as , where and are integers and is not divisible by the square of any prime. Find .
Solution:
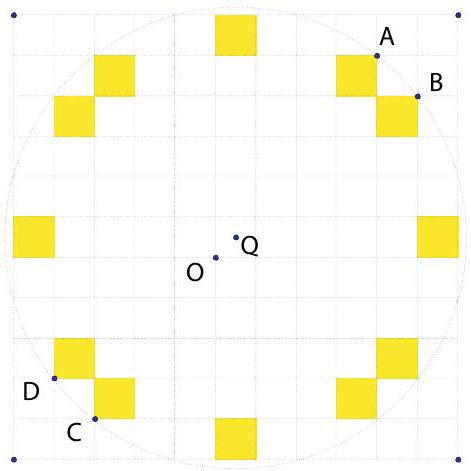
Suppose . Because takes integer values and , the ordered pairs must be elements of the set
Thus region is a subset of the unit-square regions with lower left corners in .
Region is symmetric about point . Points lie on the boundary of region . Thus is a rectangle centered at . The smallest circle that can be drawn to cover these four points (which are boundary points of ) is the circumcircle of , which has diameter . Substitution of the vertices of the twelve unit square regions into the inequality defining this circumcircle and its interior confirms that this circle does cover region . Hence the minimum value of is , and .
The problems on this page are the property of the MAA's American Mathematics Competitions