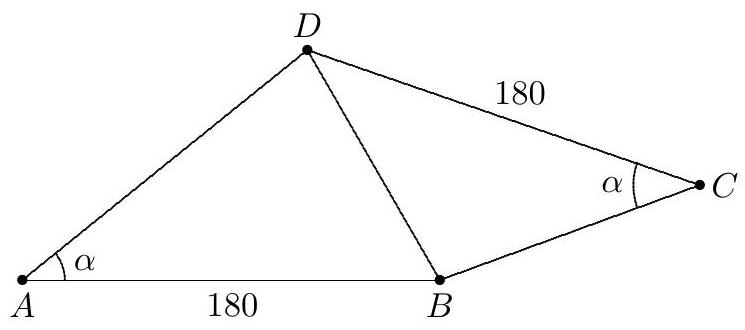
Problem:
In convex quadrilateral ABCD,∠A≅∠C,AB=CD=180, and AD=BC. The perimeter of ABCD is 640 . Find ⌊1000cosA⌋. (The notation ⌊x⌋ means the greatest integer that is less than or equal to x.)
Solution:
Let ∠A=∠C=α,AD=x, and BC=y. Apply the Law of Cosines in triangles ABD and CDB to obtain
BD2=x2+1802−2⋅180xcosα=y2+1802−2⋅180ycosα
Because x=y, this yields
cosα=2⋅180(x−y)x2−y2=360x+y=360280=97
Thus ⌊1000cosA⌋=777.
OR
Assume without loss of generality that AD is the greater of AD and BC. Then there is a point P on AD with AP=BC. Because △BAP≅△DCB, conclude that BP=BD, and altitude BH of isosceles △BPD bisects PD. Now cosA= AH/180, and because AH=AP+(PD/2)=AD−(PD/2),
AH=2AP+AD=2BC+AD=2640−2⋅180=140
Thus cosA=140/180=7/9, and ⌊1000cosA⌋=777.
The problems on this page are the property of the MAA's American Mathematics Competitions