Problem:
Circles of radii , and are mutually externally tangent, where and are relatively prime positive integers. Find .
Solution:
Let , and be the centers of the circles of radii , and , respectively. It is clear that lies outside the strip bounded by the parallel lines that are tangent to both of the circles of radius . Thus lies inside triangle , as in the figure at right. Notice that, because the centers of two tangent circles are collinear with their point of tangency, , and . Because is on the perpendicular bisector of , where is the midpoint of . Apply the Pythagorean Theorem to triangle to find that , hence that . Now apply the Pythagorean Theorem again, this time to triangle , to find that
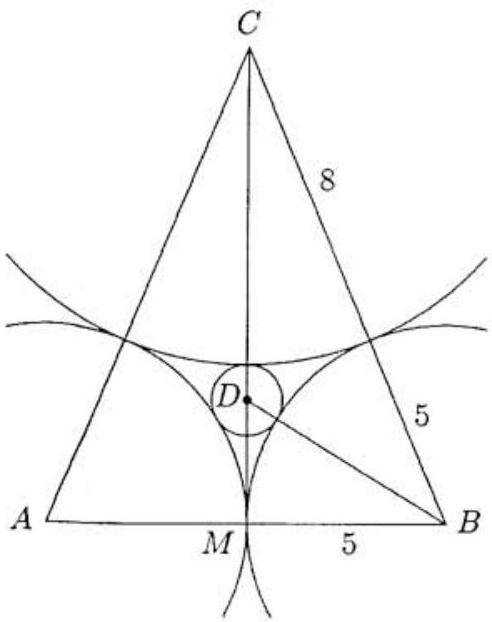
The solution to this equation is , hence .
Query. Given three mutually externally tangent circles, whose radii are , under what conditions will there be more than one circle that is externally tangent to all three circles?
The problems on this page are the property of the MAA's American Mathematics Competitions