Problem:
A rectangle has sides of length and . A hinge is installed at each vertex of the rectangle and at the midpoint of each side of length . The sides of length can be pressed toward each other keeping those two sides parallel so the rectangle becomes a convex hexagon as shown. When the figure is a hexagon with the sides of length parallel and separated by a distance of , the hexagon has the same area as the original rectangle. Find .
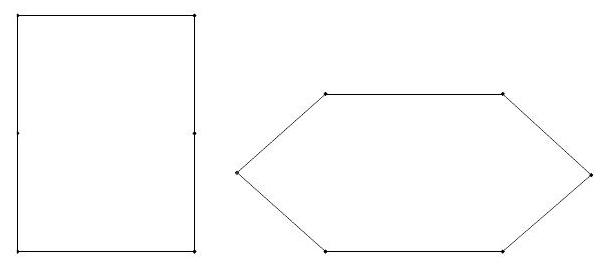
Solution:
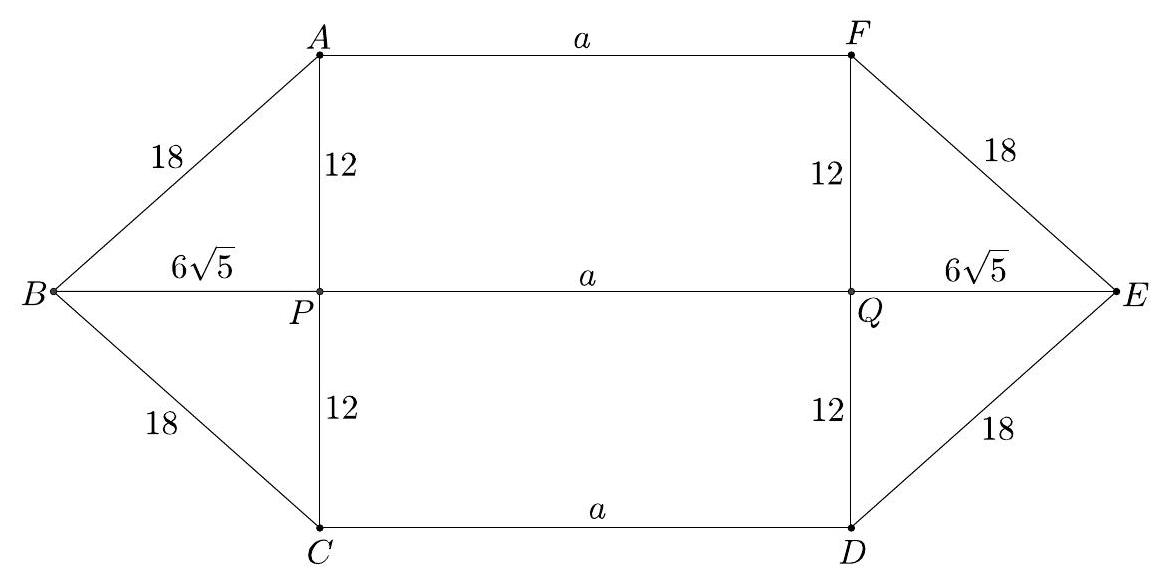
Let the vertices of the hexagon be labeled with , and let the intersections of and with be and , respectively. See the figure below. With , the hexagon has the same area as the rectangle, which is . It follows by the Pythagorean Theorem that . The area of the hexagon can be calculated by finding twice the area
of trapezoid , so
Solving yields , so .
The problems on this page are the property of the MAA's American Mathematics Competitions