Problem:
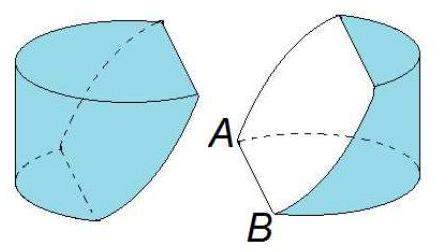
A block of wood has the shape of a right circular cylinder with radius and height , and its entire surface has been painted blue. Points and are chosen on the edge of one of the circular faces of the cylinder so that on that face measures . The block is then sliced in half along the plane that passes through point , point , and the center of the cylinder, revealing a flat, unpainted face on each half. The area of one of these unpainted faces is , where , and are integers and is not divisible by the square of any prime. Find .
Solution:
Orient the (uncut) block so that the circular face containing and rests on the floor. Let be the center of the cylinder, let be the midpoint of segment , and let be the region whose area must be computed.
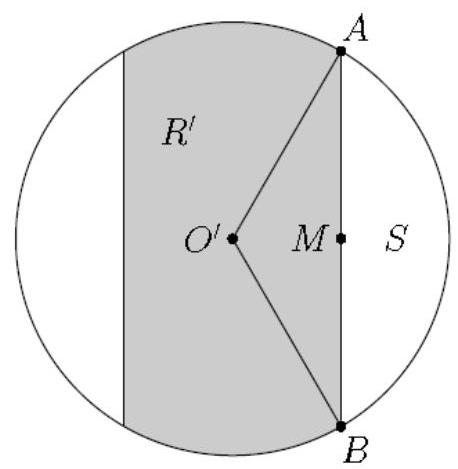
Project the diagram into the plane of the bottom face; point projects to , the center of the bottom face, and region projects to region as shown. The circular segment enclosed by chord and minor arc may be created by removing from sector , so has area . Thus region has area .
Because is a right triangle, . Because and is a right triangle, . Because is the orthogonal projection of , the two are related by a stretch in the direction perpendicular to the floor: stretching region by a factor of in the direction (and by a factor of in the direction parallel to ) results in a shape congruent to region . Thus the area of is the area of , so the area of is . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions