Problem:
A circle with radius is externally tangent to a circle with radius . Find the area of the triangular region bounded by the three common tangent lines of these two circles.
Solution:
More generally, let the larger circle have radius and center and the smaller circle have radius and center . Let the two circles be tangent at , let the common external tangents intersect at , let one of those tangents be tangent to the larger circle at and to the smaller circle at , let that tangent intersect the common internal tangent at , and let , as shown.
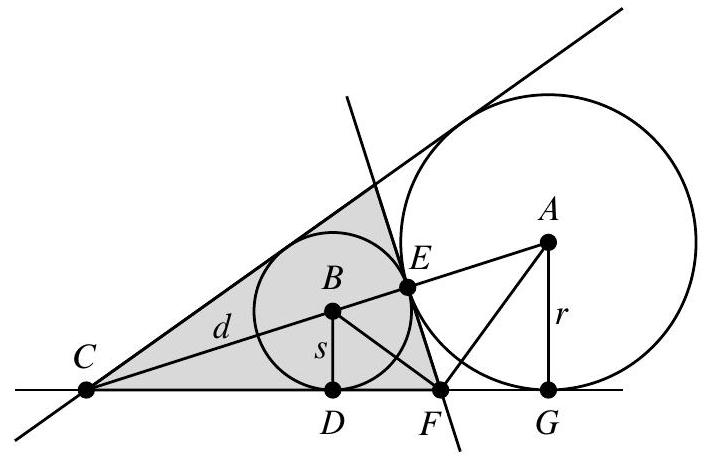
Because and are similar,
from which
Because and are supplementary, and and bisect these angles, is a right triangle, so . The required area is then
Substituting and gives
The problems on this page are the property of the MAA's American Mathematics Competitions