Problem:
A certain function has the properties that for all positive real values of , and that for . Find the smallest for which .
Solution:
First calculate
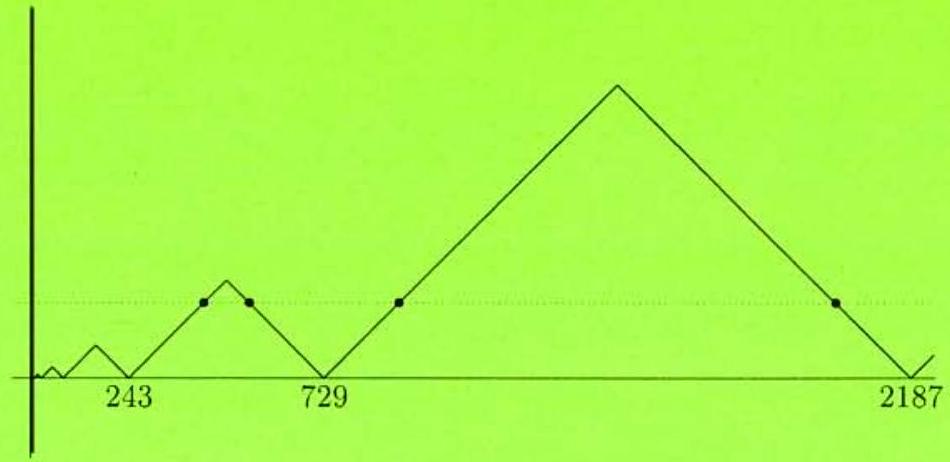
For , the graph of consists of segments that join to and to . The definition of implies that is on the graph of whenever is, so the positive -axis and the graph of form a sequence of isosceles right triangles, each a threefold magnification of its predecessor. Notice that is the altitude of the triangle whose left vertex is and whose right vertex is . Because the line intersects only those triangles whose altitudes are at least 186, the leftmost intersection point is found, as shown, in the triangle whose left vertex is and whose right vertex is . The desired point is found on a segment of slope , so .
The problems on this page are the property of the MAA's American Mathematics Competitions