Problem:
A rectangular box has width inches, length inches, and height inches, where and are relatively prime positive integers. Three faces of the box meet at a corner of the box. The center points of those three faces are the vertices of a triangle with an area of square inches. Find .
Solution:
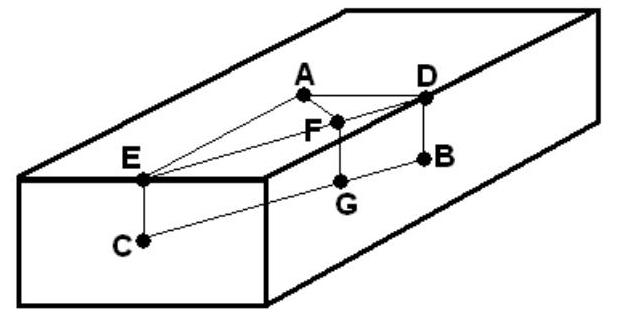
Let the box have height . Let be the center of the face, be the center of the face, and be the center of the face. Let be the midpoint of the edge of the box common to the face containing and the face containing , and let be the midpoint of the edge of the box common to the faces containing and . Let be the foot of the altitude to of , and be the foot of the altitude to of . Because and . The area , so . Similarly, , so . Note that the projection of onto the face of is , so is a right triangle. It follows that or . Solving for gives . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions