Problem:
A small square is constructed inside a square of area by dividing each side of the unit square into equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure on the right. Find the value of if the area of the small square (shaded in the figure) is exactly .
.jpg)
Solution:
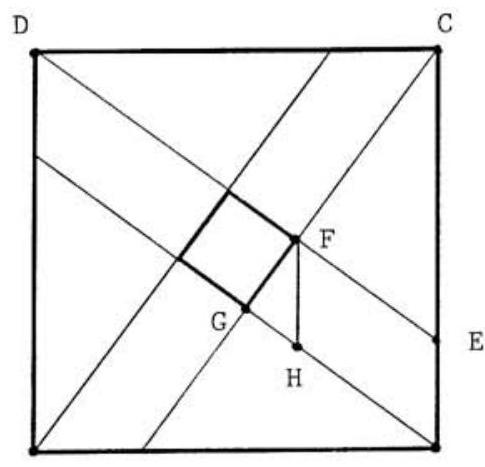
Let be the points labeled in the adjoining figure, with parallel to . Noting that is similar to , it then follows that
from which
In view of the given information, this is equivalent to
from which
Since this last equation is equivalent to , and since is positive, it follows that .
The problems on this page are the property of the MAA's American Mathematics Competitions