Problem:
Let be a triangle with sides , and , and be a -by- rectangle. A segment is drawn to divide triangle into a triangle and a trapezoid , and another segment is drawn to divide rectangle into a triangle and a trapezoid such that is similar to and is similar to . The minimum value of the area of can be written in the form , where and are relatively prime positive integers. Find .
Solution:
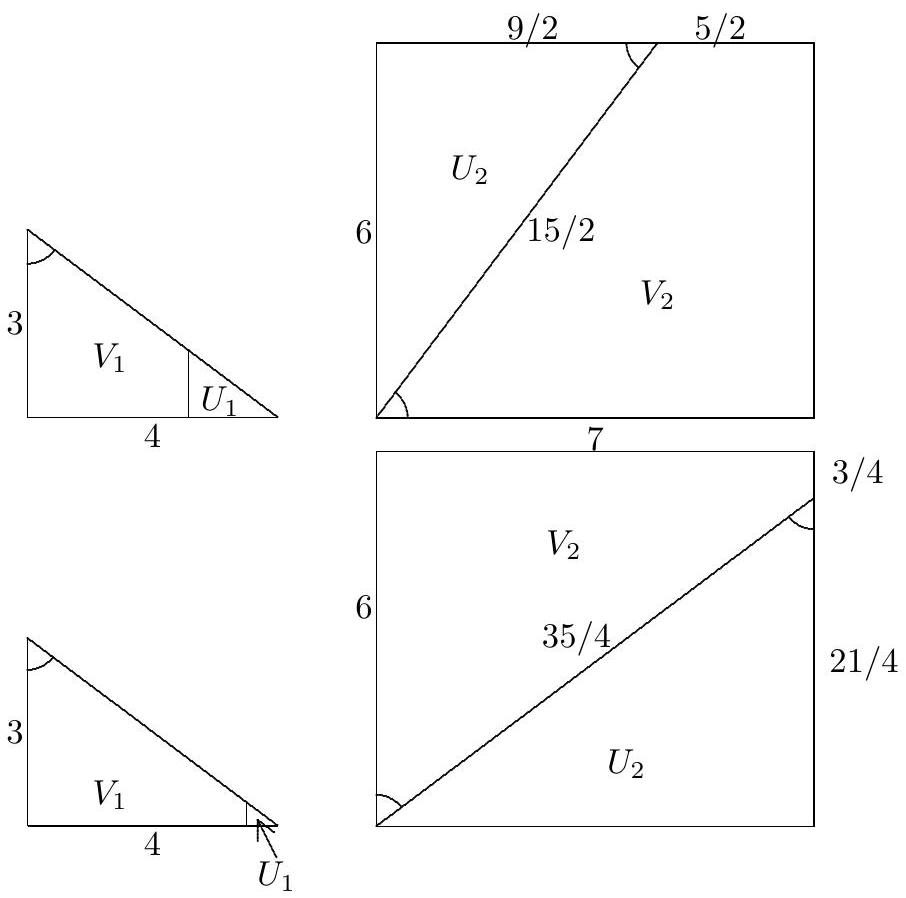
Let be the line segment drawn in , and let be the line segment drawn in rectangle . To obtain a triangle and a trapezoid, line segment must pass through exactly one vertex of rectangle . Hence is a trapezoid with a right angle, and is a right triangle. Therefore line segment is parallel to one of the legs of and, for all placements of is similar to . It follows that there are two possibilities for triangle : one in which the sides are , and ; and the other in which the sides are , , and . Were parallel to the side of length , trapezoids and could not be similar, because the corresponding acute angles in and would not be congruent; but when is parallel to the side of length , the angles of trapezoid are congruent to the corresponding angles of , so it is possible to place segment so that is similar to . In the case when the triangle has sides , and , the bases of trapezoid are and , so its bases, and therefore the bases of , are in the ratio . Then the area of triangle is . In the case when the triangle has sides , and , the bases of trapezoid are and , so its bases, and the bases of , are in the ratio . The area of triangle is then . The minimum value of the area of is thus , and .
The problems on this page are the property of the MAA's American Mathematics Competitions