Problem:
The sides of rectangle have lengths and . An equilateral triangle is drawn so that no point of the triangle lies outside . The maximum possible area of such a triangle can be written in the form , where , and are positive integers, and is not divisible by the square of any prime number. Find .
Solution:
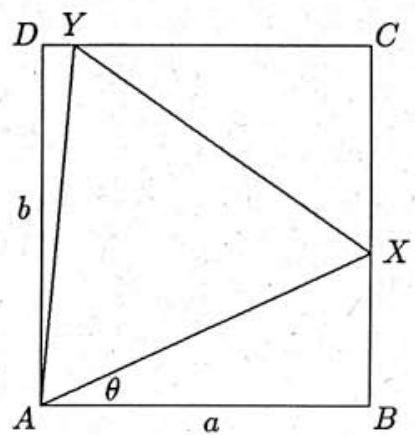
Let us generalize the problem slightly. Label the rectangle so that and . We first show that, given any equilateral triangle in , there is an equilateral triangle in that has the same area as and that has one vertex at a vertex of . Given a side of , find the vertex of that is closest to the side, then draw a line through the vertex parallel to that side. When this is done for all four sides of , we have a rectangle that encloses . One vertex of must coincide with a vertex of , because each side of passes through a vertex of . Keeping rectangle \mathcal
inside rectangle , we can slide and so that this vertex of coincides with a vertex of . It is therefore no loss of generality to assume that has a vertex at .
If an equilateral triangle exists that has on and on , then has maximal area among all equilateral triangles that lie inside . The reason is that any other equilateral triangle with a vertex at either must have a vertex that lies in or on triangle or must have a vertex that lies in or on triangle ; this implies a smaller area.
To see that such a triangle exists, and to find its area, let and be points on and , respectively, such that is a -degree angle. Let , so that and . Triangle is equilateral if and only if , which is equivalent to , which, according to the subtraction law for cosines, is equivalent to . That is, , which lies between and if and only if lies between and . Because , equilateral triangle exists. Furthermore, the area of triangle is
which simplifies to . Hence .
The problems on this page are the property of the MAA's American Mathematics Competitions