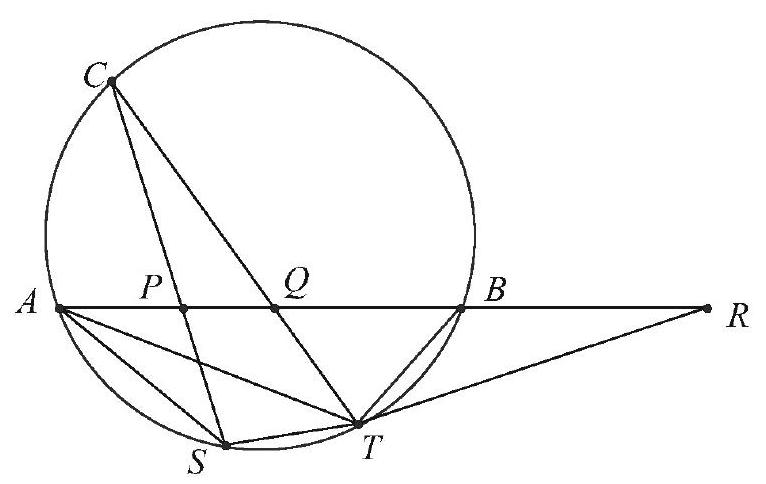
Problem:
Triangle ABC is inscribed in circle ω. Points P and Q are on side AB with AP<AQ. Rays CP and CQ meet ω again at S and T (other than C ), respectively. If AP=4,PQ=3,QB=6,BT=5, and AS=7, then ST=nm​, where m and n are relatively prime positive integers. Find m+n.
Solution:
Extend AB through B to R so that BR=8. Because ACBT is cyclic, it follows by the Power of a Point Theorem that CQâ‹…QT=AQâ‹…QB=42. Note that PQâ‹…QR=42=CQâ‹…QT. By the converse of the Power of a Point Theorem, it follows that CPTR is cyclic. Because CPTR and ACTS are cyclic,
∠BRT=∠PRT=∠PCT=∠SCT=∠SAT.
Because ABTS is cyclic, it follows that ∠AST=∠RBT. Hence △AST is similar to △RBT, from which STAS​=BTRB​ or ST=AS⋅RBBT​=835​. The requested sum is 35+8=43​.
The problems on this page are the property of the MAA's American Mathematics Competitions
