Problem:
A cylindrical barrel with radius feet and height feet is full of water. A solid cube with side length feet is set into the barrel so that the diagonal of the cube is vertical. The volume of water thus displaced is cubic feet. Find .
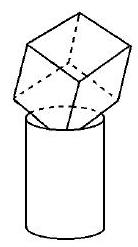
Solution:
The region inside the cube sitting inside the barrel is a right triangular pyramid with an equilateral triangle for a base and three other faces that are congruent right isosceles triangles. The center of the equilateral triangular base is the center of the circle at the top of the barrel. Because the barrel has radius , the equilateral triangle has side length and altitude . It follows that the legs of the isosceles right triangular faces of the pyramid have length . The volume of the displaced water is the volume of the pyramid. Reorienting the pyramid so that its base is a right isosceles triangle with legs of length , and its height is shows that the volume is . The requested value is .
The problems on this page are the property of the MAA's American Mathematics Competitions