Problem:
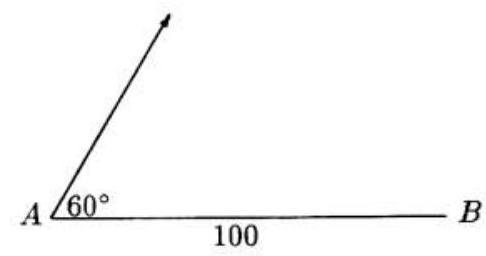
Two skaters, Allie and Billie, are at points and , respectively, on a flat, frozen lake. The distance between and is meters. Allie leaves and skates at a speed of meters per second along a straight line that makes an angle of with , as shown. At the same time that Allie leaves , Billie leaves at a speed of meters per second and follows the straight line path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?
Solution:
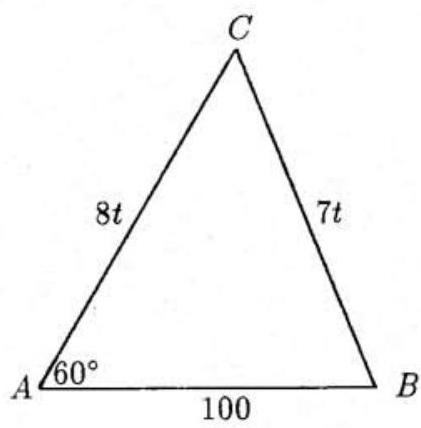
Suppose that after seconds, Allie and Billie meet at point . Then has sides of and , with opposite the angle. Hence, by the Law of Cosines,
from which
Thus or . Since the meeting takes place at the earliest possible time, we must have and hence meters.
The problems on this page are the property of the MAA's American Mathematics Competitions