Problem:
The diagram below shows a rectangular array of points, each of which is unit away from its nearest neighbors. Define a growing path to be a sequence of distinct points of the array with the property that the distance between consecutive points of the sequence is strictly increasing. Let be the maximum possible number of points in a growing path, and let be the number of growing paths consisting of exactly points. Find .

Solution:
The following argument shows that and . Note that the square of any distance between distinct points in the array has the form for some integers and in the set with and not both equal to . There are such possible values, namely, , and . Hence a growing path can consist of at most points. It remains to show that points can be so chosen, and that there are such paths. Let the points of these paths be labeled . First, must be ; that is, and must be a pair of opposite corners in the array. There are equivalent ways to label and . Without loss of generality, assume that and are the bottom right corner and upper left corner, respectively. Then there are symmetrical positions for , both neighboring . (See the left-hand diagram below.) Assume that is beside , as shown in the middle diagram below.
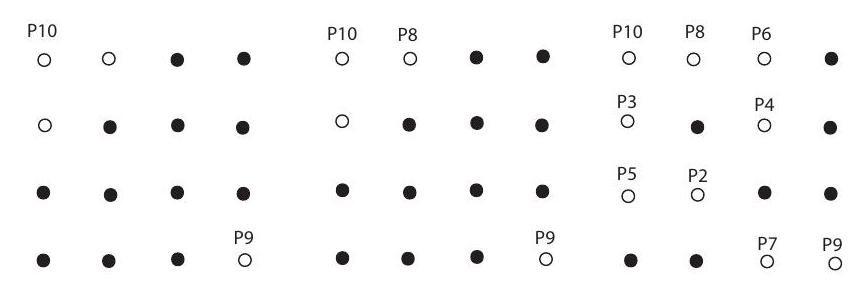
Note that the bottom left corner cannot be , because otherwise or . The positions of points , and are then fixed. (See the right-hand diagram above.) Finally, there are possible positions for . Hence , and .
The problems on this page are the property of the MAA's American Mathematics Competitions