Problem:
In the middle of a vast prairie, a fire truck is stationed at the intersection of two perpendicular straight highways. The truck travels at miles per hour along the highways and at miles per hour across the prairie. Consider the set of points that can be reached by the fire truck within six minutes. The area of this region is square miles, where and are relatively prime positive integers. Find .
Solution:
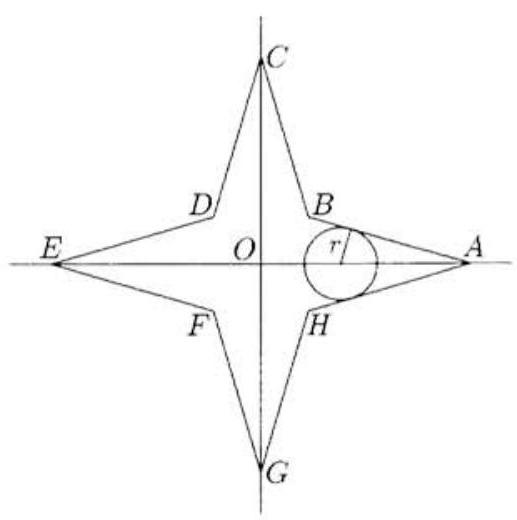
Set up a coordinate system in which the axes coincide with the highways. The points that can be reached within six minutes lie on or within circles of radius centered at points or on the axes, where . The radius of each circle is thus linearly related to . the distance from its center to the origin ; namely , or . Given any onc of the circles centered on the positive -axis. is the sine of the angle formed by the -axis and a tangent drawn from . It follows that these circles share two common external tangent lines, and that the region in question is a nonconvex octagon , where is in the first quadrant. Notice that is on the line , which is one of the four axes of symmetry of the region. An equation for the common external tangent is , because . Set to find that . The area of is times the area of , or . Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions