Problem:
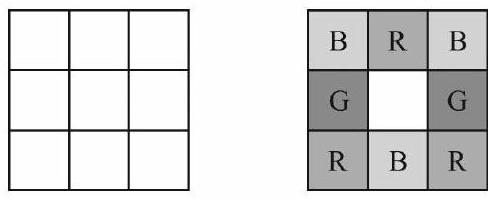
Each square in a grid of squares is colored red, white, blue, or green so that every square contains one square of each color. One such coloring is shown on the right below. How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Label the squares as shown.
There are four squares that need to satisfy the condition: abde, bcef, degh, and ef hi.
- Square : There are ways to color these squares using all four colors.
- Square : Since squares and have already been colored, either receives the same color as and receives the same color as , or these are switched. This gives 2 choices at this stage. Using the numbers , and 4 to represent the colors, the two possibilities are pictured below.
- Remaining squares on the bottom row: Squares and have already been colored. If and have the same color, then there are two ways to color the three remaining squares:
On the other hand, if squares and receive different colors, then there is only one way to color the bottom row:
Thus the number of colorings is .
The problems on this page are the property of the MAA's American Mathematics Competitions