Problem:
Two points on the circumference of a circle of radius are selected independently and at random. From each point a chord of length is drawn in a clockwise direction. What is the probability that the two chords intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
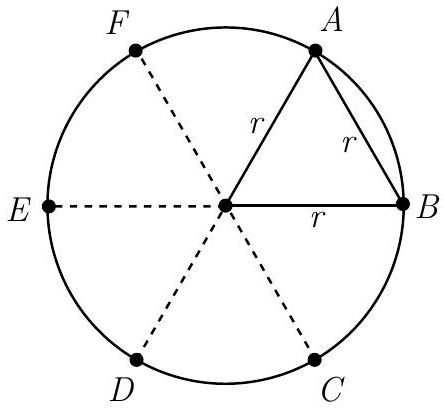
Let point be the first point chosen, and let point be the opposite endpoint of the corresponding chord. Drawing a radius to each endpoint of this chord of length results in an equilateral triangle. Hence a chord of length subtends an arc the circumference of the circle. Let diameter be parallel to , and divide the circle into six equal portions as shown. The second point chosen will result in a chord that intersects if and only if the point is chosen from minor . Hence the probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions