Problem:
Real numbers and are chosen independently and uniformly at random from the interval . Which of the following numbers is closest to the probability that , and are the side lengths of an obtuse triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
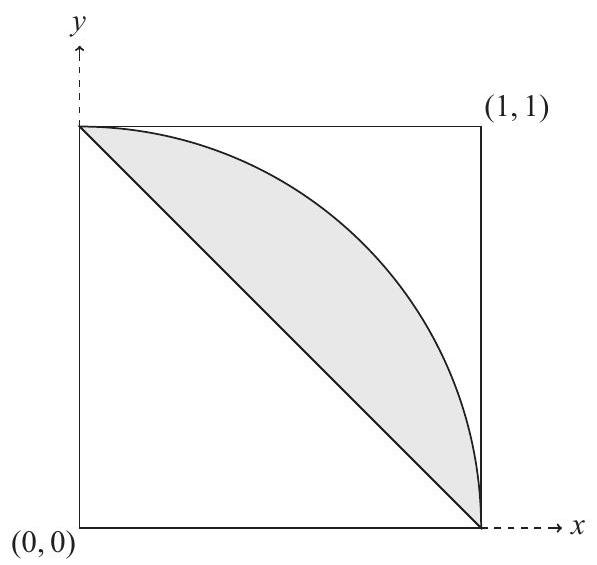
The set of all possible ordered pairs occupies the unit square in the Cartesian plane. The numbers , and are the side lengths of a triangle if and only if , which means that lies above the line . By a generalization of the Pythagorean Theorem, the triangle is obtuse if and only if, in addition, , which means that lies inside the circle of radius centered at the origin. Within the unit square, the region inside the circle of radius centered at the origin has area , and the region below the line has area . Therefore the ordered pairs that meet the required conditions occupy a region with area . The area of the unit square is , so the required probability is also , which is closest to .
The problems on this page are the property of the MAA's American Mathematics Competitions