Problem:
The interior of a quadrilateral is bounded by the graphs of and , where is a positive real number. What is the area of this region in terms of , valid for all ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
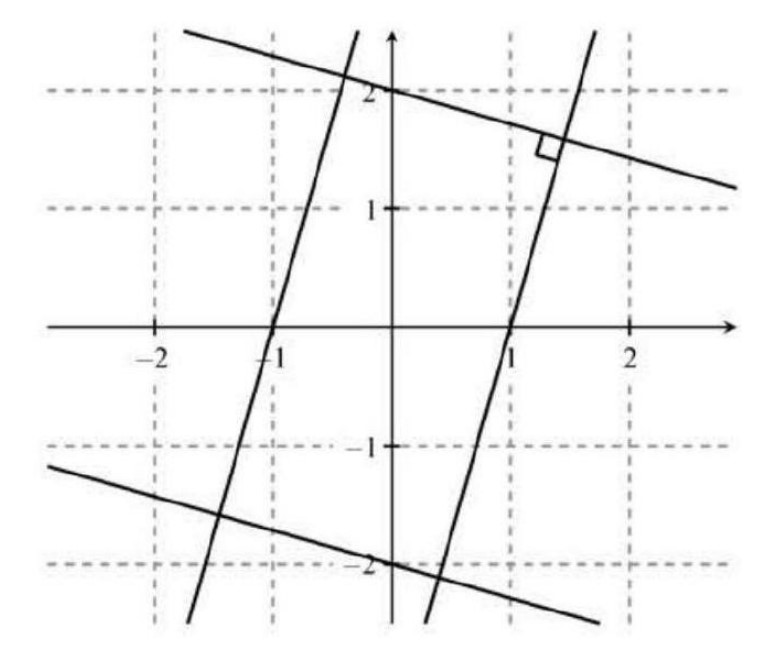
Taking the positive and negative square roots of both sides of these equations shows that this region is bounded by the graphs of four lines: and . Because their slopes are negative reciprocals of each other, lines and are perpendicular, as are lines and . Therefore the region bounded by these lines is the interior of a rectangle.
The distance between two parallel lines and is
Thus the distance between the first two lines is
The distance between the last two lines is
The area of the rectangle is the product of these two distances,
Note: The shape of the rectangle depends on . The graph below shows the situation when , with area of approximately
The problems on this page are the property of the MAA's American Mathematics Competitions