Problem:
Two circles lie outside regular hexagon . The first is tangent to , and the second is tangent to . Both are tangent to lines and . What is the ratio of the area of the second circle to that of the first circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
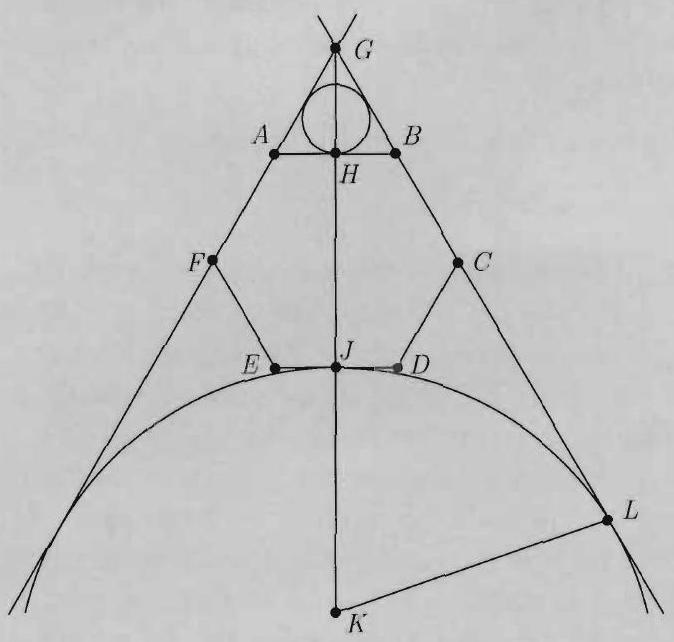
It may be assumed that hexagon has side length . Let lines and intersect at , let and be the midpoints of and , respectively, let be the center of the second circle, and let that circle be tangent to line at . Equilateral has side length , so the first circle, which is the inscribed circle of , has radius . Let be the radius of the second circle. Then is a right triangle with and . Therefore . The ratio of the radii of the two circles is , and the ratio of their areas is .
The problems on this page are the property of the MAA's American Mathematics Competitions