Problem:
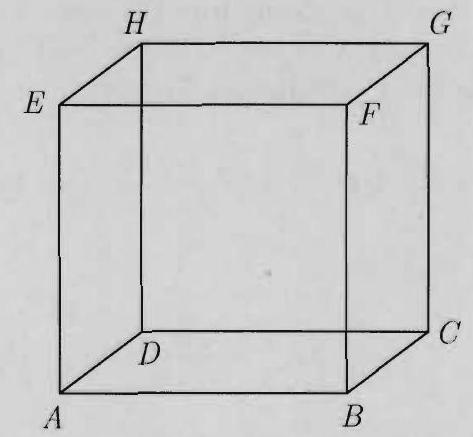
A fly trapped inside a cubical box with side length meter decides to relieve its boredom by visiting each corner of the box. It will begin and end in the same corner and visit each of the other corners exactly once. To get from a corner to any other corner, it will either fly or crawl in a straight line. What is the maximum possible length, in meters, of its path?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Each of the lines segments on the fly's path is an edge, a face diagonal, or an interior diagonal of the cube. These three type of line segments have lengths , and , respectively. Because each vertex of the cube is visited only once, the two line segments that meet at a vertex have a combined length of at most . Therefore the sum of the lengths of the segments is at most . This maximum is achieved by the path
The problems on this page are the property of the MAA's American Mathematics Competitions