Problem:
Each square in a grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
Any filled square with two or three filled neighbors remains filled. Any empty square with exactly three filled neighbors becomes a filled square. All other squares remain empty or become empty. A sample transformation is shown in the figure below.
.jpg)
.jpg)
Initial Transformed
Suppose the grid has a border of empty squares surrounding a subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
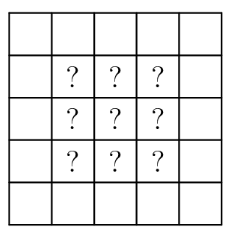
.jpg)
Initial Transformed
Answer Choices:
A.
B.
C.
D.
E.
Solution:
If the center square is filled, then in order for it to remain filled either two or three of the eight neighboring squares must be filled. If two of these are in the middle horizontal or vertical row then a noncentral square would become filled. Now suppose that exactly one of these is in the middle horizontal or vertical row and there is one other square that is filled. By symmetry, there are only two cases to consider, and in each of these cases a noncentral square would become filled. If exactly one of these filled squares is in the middle horizontal or vertical row and there are two other squares that are filled, a noncentral square would also become filled. Therefore the only possibility in this case is the one shown in the first diagram below or a rotation of that diagram.
If the center square is not filled, then in order for it to become filled exactly three of the eight neighboring squares must be filled. The only case (up to rotation) in which two of them are diagonally adjacent is shown in the second diagram below. The two cases up to rotation in which none of these three filled-in squares are adjacent are shown in the next two diagrams below. Finally,
if two squares of the filled-in squares are adjacent along an edge, then the configuration must look like the fifth diagram below, up to rotation or reflection.
.jpg)
By symmetry, the first pattern corresponds to 2 configurations, the next 3 patterns correspond to 4 configurations each, and the last pattern corresponds to 8 configurations, for a total of . configurations.
Note: This problem is based on the cellular automaton Game of Life, created by John Conway (1937-2020).
The problems on this page are the property of the MAA's American Mathematics Competitions