Problem:
Six regular hexagonal blocks of side length unit are arranged inside a regular hexagonal frame. Each block lies along an inside edge of the frame and is aligned with two other blocks, as shown in the figure below. The distance from any corner of the frame to the nearest vertex of a block is unit. What is the area of the region inside the frame not occupied by the blocks?
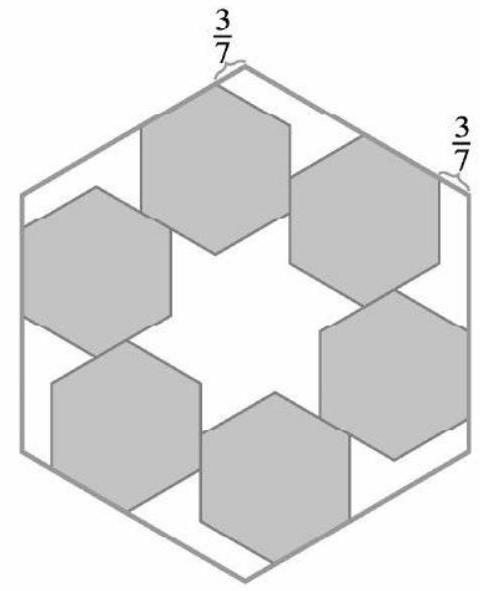
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The required area equals the difference between the area enclosed by the hexagonal frame and the area of the 6 hexagonal blocks. A block is composed of 6 unit equilateral triangles, each of area square units, so the 6 blocks have a total area of square units.
Let represent the distance from a corner of the frame to the nearest block vertex. To determine the side length of the frame, extend the sides of any block beyond the frame border, as shown below, to form a unit equilateral triangle and a smaller equilateral triangle of side length .
.jpg)
Each empty region along the border of the frame can be divided into a unit equilateral triangle and a trapezoid with bases of lengths 1 and . Thus the frame has a side length of units and encloses an area of square units. The required area is square units. Note that the value of is irrelevant.
The required area equals the difference between the area enclosed by the hexagonal frame and the area of the 6 hexagonal blocks. A block is composed of 6 unit equilateral triangles, each of area square units, so the 6 blocks have a total area of square units.
To determine the side length of the hexagonal frame, note that the blocks can be shifted simultaneously without altering the size of the frame. Consider the arrangement shown below.
.jpg)
If the blocks are moved to the centers of the frame edges, there will be an empty rhombus of side length 1 unit at each corner of the frame. It follows that the side length of the frame is units and encloses an area of square units. Thus the required area is square units.
The problems on this page are the property of the MAA's American Mathematics Competitions