Problem:
A point is chosen at random within the square in the coordinate plane whose vertices are , and . The probability that the point lies within units of a lattice point is . (A point is a lattice point if and are both integers.) What is to the nearest tenth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
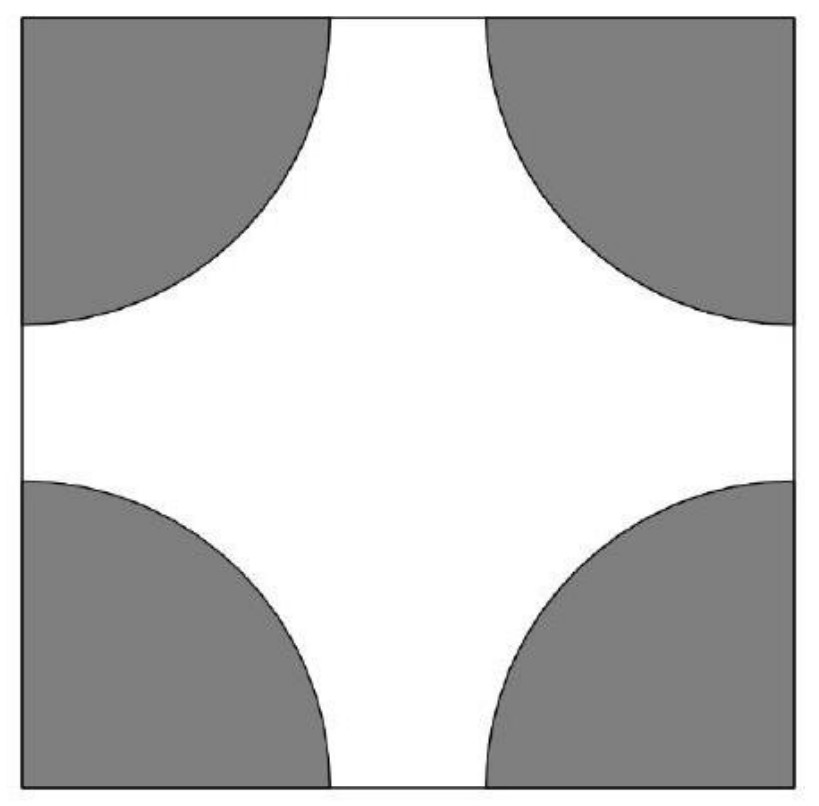
The diagram represents each unit square of the given square.
We consider an individual one-by-one block. If we draw a quarter of a circle from each corner (where the lattice points are located), each with radius , the area covered by the circles should be . Because of this, and the fact that there are four circles, we write
Solving for , we obtain
and from here, we see that
Note: To be more rigorous, note that since if then clearly the probability is greater than . This would make sure the above solution works as if there is overlap with the quarter circles.
As in the previous solution, we obtain the equation
which simplifies to
Since is slightly more than is slightly less than . We notice that is slightly more than , so
The problems on this page are the property of the MAA's American Mathematics Competitions