Problem:
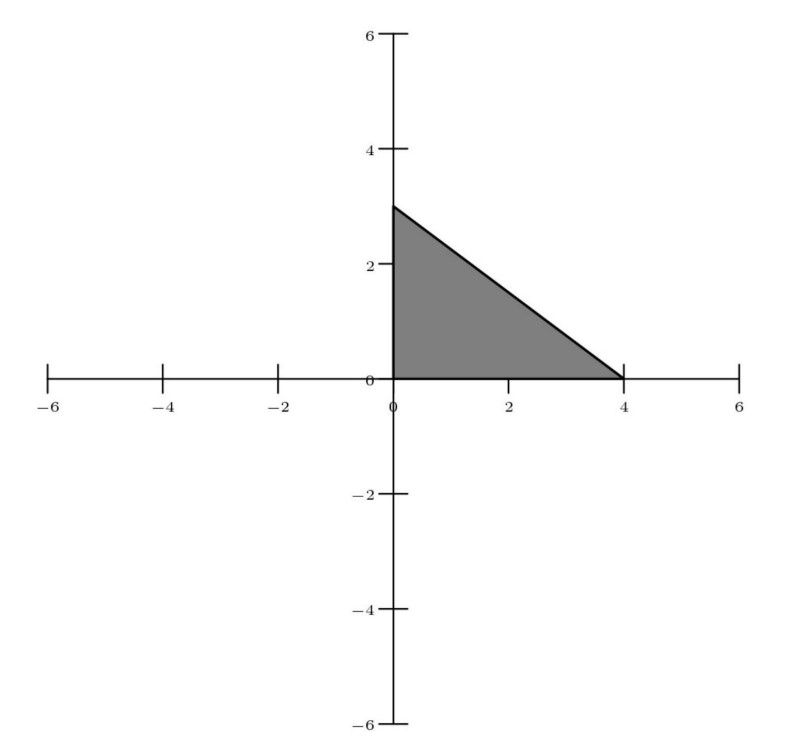
Let be the triangle in the coordinate plane with vertices , , and . Consider the following five isometries (rigid transformations) of the plane: rotations of , and counterclockwise around the origin, reflection across the -axis, and reflection across the -axis. How many of the 125 sequences of three of these transformations (not necessarily distinct) will return to its original position? (For example, a rotation, followed by a reflection across the -axis, followed by a reflection across the -axis will return to its original position, but a rotation, followed by a reflection across the -axis, followed by another reflection across the -axis will not return to its original position.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First, any combination of motions we can make must reflect an even number of times. This is because every time we reflect , it changes orientation. Once has been flipped once, no combination of rotations will put it back in place because it is the mirror image; however, flipping it again changes it back to the original orientation. Since we are only allowed 3 transformations and an even number of them must be reflections, we either reflect times or times.
-
Case 1: reflections on .
In this case, we must use rotations to return to its original position. Notice that our set of rotations, , contains every multiple of except for . We can start with any two rotations in and there must be exactly one such that we can use the three rotations which ensures that . That way, the composition of rotations yields a full rotation. For example, if , then , so and the rotations yields a full rotation.The only case in which this fails is when would have to equal . This happens when is already a full rotation, namely, , or . However, we can simply subtract these three cases from the total. Selecting from yields choices, and with that fail, we are left with combinations for case .
-
Case 2: reflections on . In this case, we first eliminate the possibility of having two of the same reflection. Since two reflections across the -axis maps back to itself, inserting a rotation before, between, or after these two reflections would change 's final location, meaning that any combination involving two reflections across the -axis would not map back to itself. The same applies to two reflections across the -axis.
Therefore, we must use one reflection about the -axis, one reflection about the -axis, and one rotation Since a reflection about the -axis changes the sign of the component, a reflection about the -axis changes the sign of the component, and a rotation changes both signs, these three transformations composed (in any order) will suffice. It is therefore only a question of arranging the three, giving us combinations for case .
Combining both cases we get
Define as a reflection, and as a counterclockwise rotation. Thus, , and the five transformations can be represented as , and .
Now either doesn't appear at all or appears twice. For the former case, it's easy to see that only and will work. Both can be permuted in ways, giving ways in total.
For the latter case, note that can't appear twice, neither does , else we need to get from , which is not possible. So and must appear once each. The last transformation must be . A quick check shows that is permutable, since (since ). This gives ways.
Thus the answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions