Problem:
Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the tops of the liquid surfaces are and . Into each cone is dropped a spherical marble of radius , which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the rise of the liquid level in the wide cone?
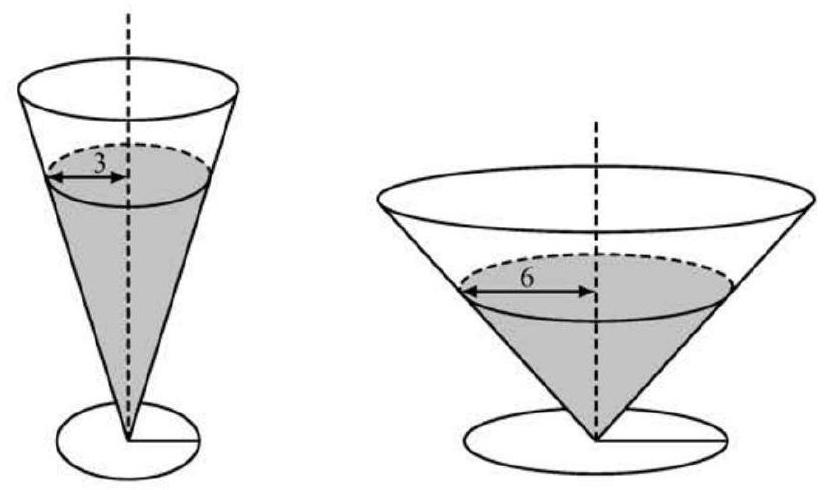
Answer Choices:
A.
B.
C.
D.
E.
Solution:
If two cones have the same volume and the radius of the narrow cone is one-half the radius of the wide cone, then because the volume of a cone varies directly with both the square of the radius and the height, it follows that the height of the narrow cone is times the height of the wide cone. The volumes of liquid are the same both before and after the marble is added, so both heights for the narrow cone are times the corresponding heights for the wide cone. Hence the rise of the level in the narrow cone is also times the rise of the level in the wide cone.
Let and be the heights of the liquid in the narrow and wide cones, respectively, before the marble is dropped in. The two equal volumes of liquid are
which implies . When the marble of volume is added, both the heights and the radii of the conical volumes of water change, but the volumes remain equal. Let and be the new radius and height for the new narrow cone, and and be the new radius and height for the new wide cone. Then
By similar triangles, . Substituting and solving for gives
Letting gives
which is equivalent to
Similarly,
and by similar triangles, . Substituting and solving for gives
It follows that the ratio of the rise of the water levels is
.
The problems on this page are the property of the MAA's American Mathematics Competitions