Problem:
There are yellow pegs, red pegs, green pegs, blue pegs, and orange peg to be placed on a triangular peg board. In how many ways can the pegs be placed so that no (horizontal) row or (vertical) column contains two pegs of the same color?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
To avoid having two yellow pegs in the same row or column, there must be exactly one yellow peg in each row and in each column. Hence, starting at the top of the array, the peg in the first row must be yellow, the second peg of the second row must be yellow, the third peg of the third row must be yellow, etc. To avoid having two red pegs in some row, there must be a red peg in each of rows and . The red pegs must be in the first position of the second row, the second position of the third row, etc. Continuation yields exactly ordering that meets the requirements, as shown.
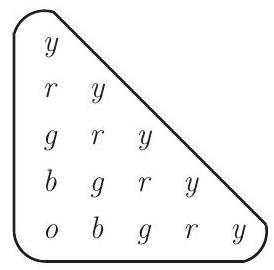
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions