Problem:
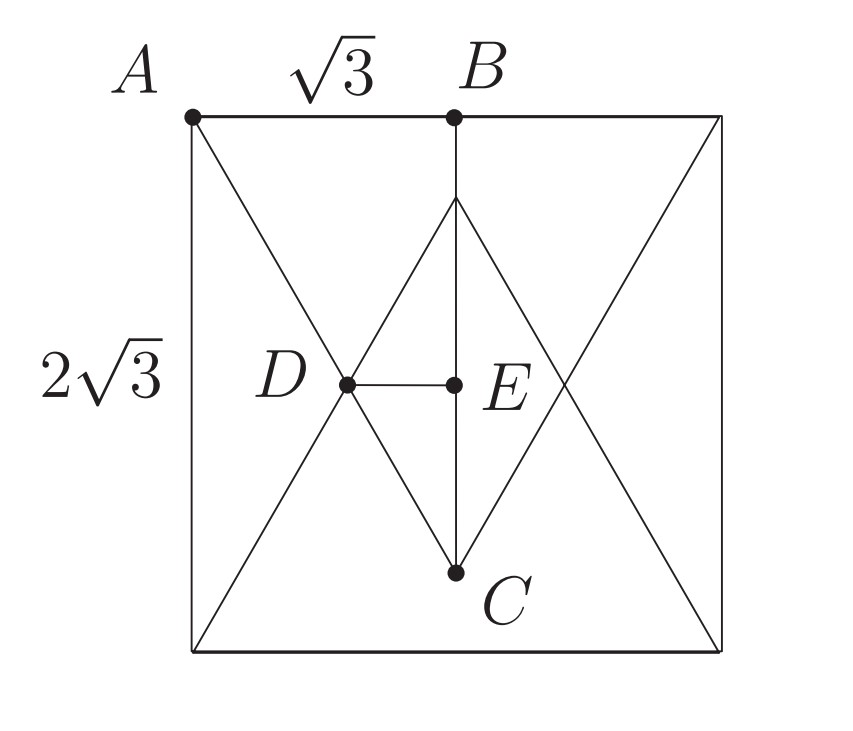
Two equilateral triangles are contained in a square whose side length is . The bases of these triangles are the opposite sides of the square, and their intersection is a rhombus. What is the area of the rhombus?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Construct the altitude for one of the equilateral triangles to its base on the square. Label the vertices of one of the resulting triangles , and , as shown. Then and . Label one of the intersection points of the two equilateral triangles and the center of the square . Then is a triangle, , and . The area of is . Hence the area of the rhombus is .
The problems on this page are the property of the MAA's American Mathematics Competitions