Problem:
A scanning code consists of a grid of squares, with some of its squares colored black and the rest colored white. There must be at least one square of each color in this grid of squares. A scanning code is called symmetric if its look does not change when the entire square is rotated by a multiple of counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
None of the squares that are marked with dots in the sample scanning code shown below can be mapped to any other marked square by reflections or non-identity rotations. Therefore these squares can be arbitrarily colored black or white in a symmetric scanning code, with the exception of "all black" and "all white". On the other hand, reflections or rotations will map these squares to all the other squares in the scanning code, so once these colors are specified, the symmetric scanning code is completely determined. Thus there are symmetric scanning codes.
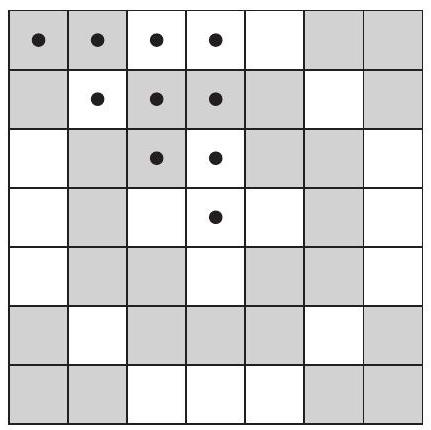
The diagram below shows the orbits of each square under rotations and reflections. Because the scanning code must look the same under these transformations, all squares in the same orbit must get the same color, but one is free to choose the color for each orbit, except for the choice of "all black" and "all white". Because there are orbits, there are symmetric scanning codes.
The problems on this page are the property of the MAA's American Mathematics Competitions