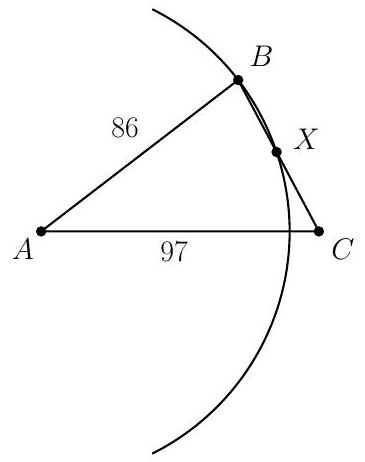
Problem:
In △ABC,AB=86, and AC=97. A circle with center A and radius AB intersects BC at points B and X. Moreover BX and CX have integer lengths. What is BC?
Answer Choices:
A. 11
B. 28
C. 33
D. 61
E. 72
Solution:
By the Power of a Point Theorem, BC⋅CX=AC2−r2 where r=AB is the radius of the circle. Thus BC⋅CX=972−862=2013. Since BC=BX+CX and CX are both integers, they are complementary factors of 2013. Note that 2013=3⋅11⋅61, and CX<BC<AB+AC=183. Thus the only possibility is CX=33 and BC=(D)61.
The problems on this page are the property of the MAA's American Mathematics Competitions