Problem:
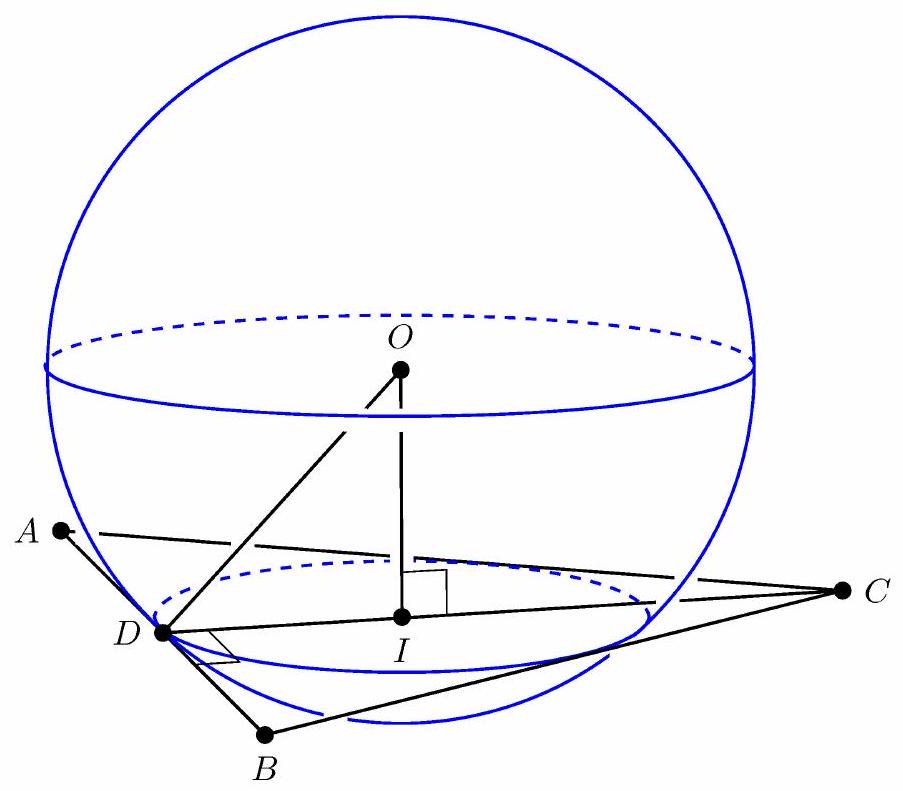
A sphere with center has radius . A triangle with sides of length and is situated in space so that each of its sides is tangent to the sphere. What is the distance between and the plane determined by the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the given triangle, with and , and let be the midpoint of . The length of the altitude to is . The area of is . The plane of the triangle intersects the sphere in a circle, which is the inscribed circle for . Let and be the radius and the center of the inscribed circle, respectively. The semiperimeter of the triangle is , so . In right triangle the hypotenuse has length (the radius of the sphere) and , so , the requested distance between the center of the sphere and the plane determined by .
The problems on this page are the property of the MAA's American Mathematics Competitions