Problem:
Inside a right circular cone with base radius 5 and height 12 are three congruent spheres each with radius . Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the center of the base of the cone, be the center of one of the spheres, be the point where that sphere is tangent to the base of the cone, be the point such that is a radius of the base of the cone containing be the vertex of the cone, and be the point on such that contains . Let the radius of the sphere be .
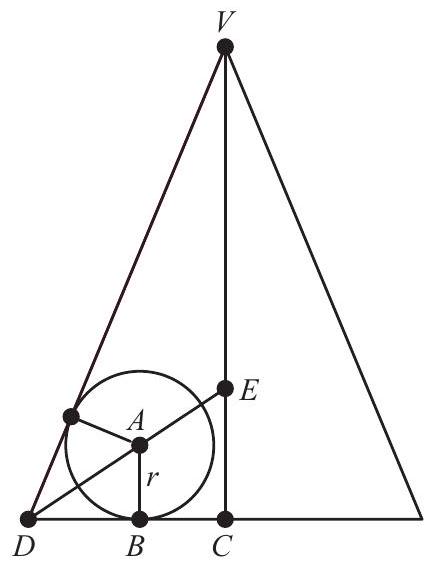
Because the three spheres are mutually tangent, their centers are at the vertices of an equilateral triangle with side length . The line passes through the centroid of the equilateral triangle, so must be the altitude of that triangle, implying that . The Pythagorean Theorem implies that 13.
Observe that is the angle bisector of . By the Angle Bisector Theorem, . Thus and solving gives . Because , it follows that
Then gives
Solving for yields .
The problems on this page are the property of the MAA's American Mathematics Competitions