Problem:
A square with side length is inscribed in an isosceles triangle with one side of the square along the base of the triangle. A square with side length has two vertices on the other square and the other two on sides of the triangle, as shown. What is the area of the triangle?
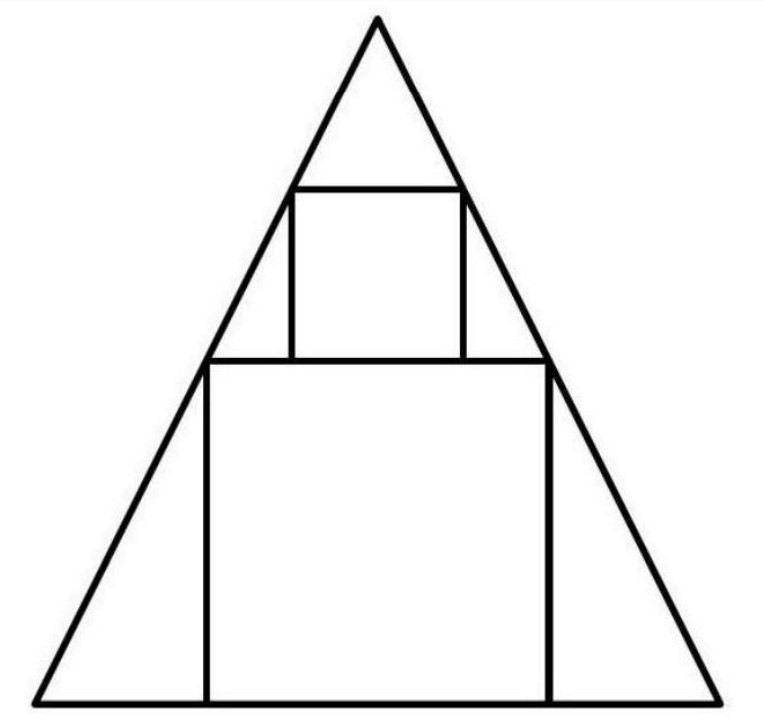
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let’s split the triangle down the middle and label it:
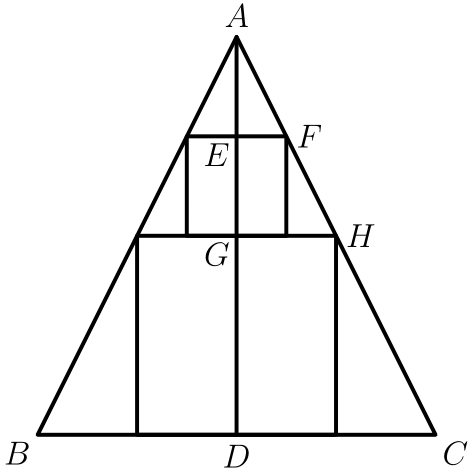
We see that by AA similarity. because cuts the side length of the square in half; similarly, . Let , then by side ratios,
Now the height of the triangle is . By side ratios,
The area of the triangle is .
The problems on this page are the property of the MAA's American Mathematics Competitions