Problem:
Three identical square sheets of paper each with side length are stacked on top of each other. The middle sheet is rotated clockwise about its center and the top sheet is rotated clockwise about its center, resulting in the -sided polygon shown in the figure below. The area of this polygon can be expressed in the form , where , and are positive integers, and is not divisible by the square of any prime. What is ?
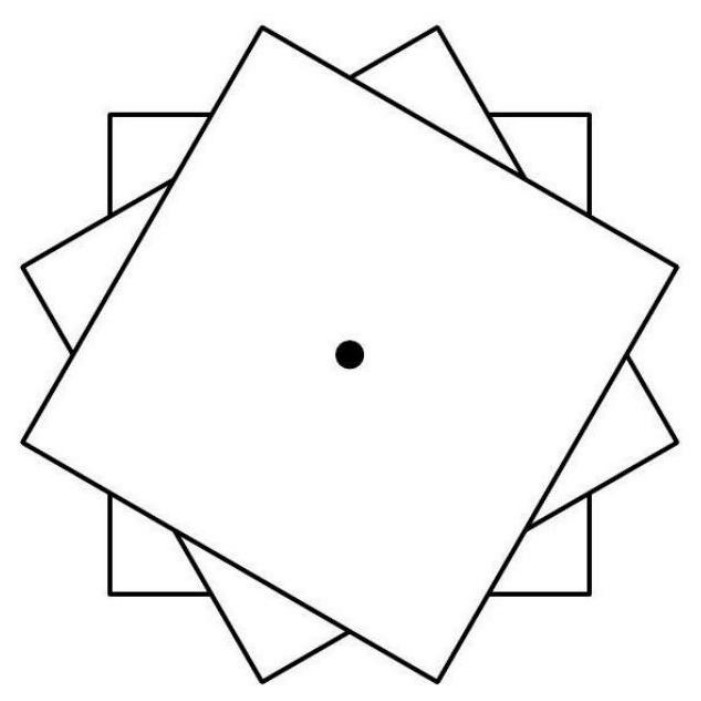
Answer Choices:
A.
B.
C.
D.
E.
Solution:
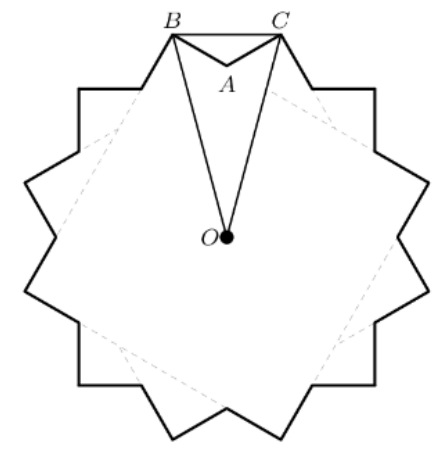
Break the -gon as shown so that there are copies of quadrilateral . We can find the area of this quadrilateral by finding the area of triangle and subtracting the area of triangle .
The angle from O to one of the vertices of the original square is , and this point rotates , so the angle that makes with the horizontal is .
Let be the intersection of with . Since and are both isosceles, forms a right angle with . Furthermore, .
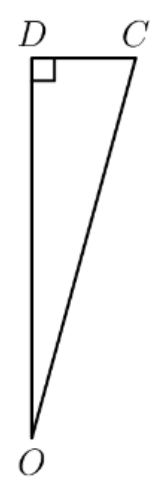
Note that is equal to because it is half the diagonal of the square with side length . We can now split up the into and triangles to find the height and length of the triangle:
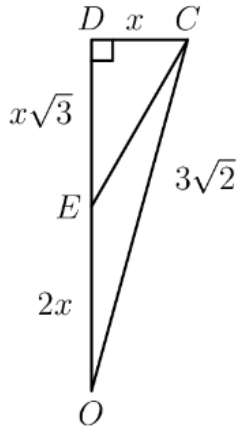
Now we have use Pythagorean: x^2+(x\cdot(2+\sqrt{3}))^2=3\sqrt{2}^2\Rightarrow x^2+x^2\cdot(7+4\sqrt{3})=18\Rightarrow x^2=\frac{18}{8+4\sqrt{3}}=\frac{9}{4 + 2\sqrt{3}}\Rightarrow x^2 = \frac{36 - 18\sqrt{3}}
Now note that x must be in the form of . Therefore, . We can guess that . Sure enough, , so . Then the height of the triangle is .
The area of triangle is equal to the length times the height of triangle since this triangle has half the area of the full triangle. Therefore the area of triangle .
Now we look at triangle . because is the diagonal of a square, and is as we saw earlier. Therefore, . Because both these angles are , .
We can now split triangle into two congruent triangles, and we know the base of each since .
The height of these triangles is . Therefore the area of this triangle is .
Therefore the total area of this segment is . Multiplying by to find the entire area, the area of the figure is and the answer is 108 + 36 + 3 = \boxed
The problems on this page are the property of the MAA's American Mathematics Competitions