Problem:
Let ABCD be a rectangle with AB=30 and BC=28. Points P and Q lie on BC and CD, respectively, so that all sides of â–³ABP,â–³PCQ, and â–³QDA have integer lengths. What is the perimeter of â–³APQ?
Answer Choices:
A. 84
B. 86
C. 88
D. 90
E. 92
Solution:
The figure below shows the given information.
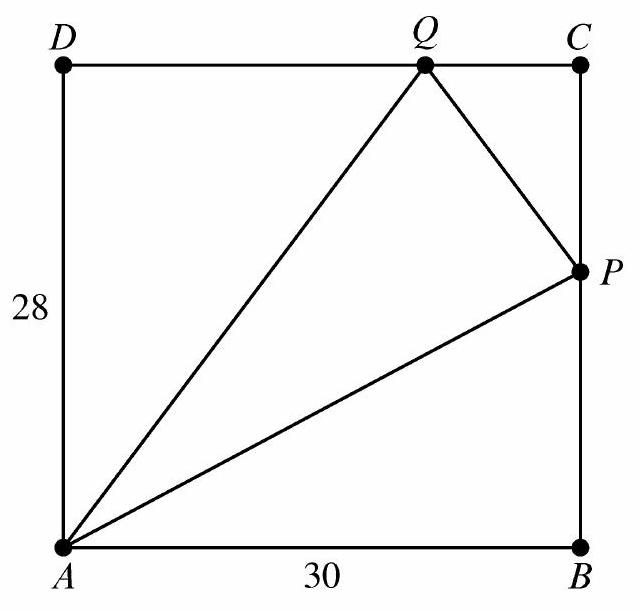
The Pythagorean triples with smallest total lengths are 3−4−5,5−12−13,7−24−25,8−15−17, and multiples thereof. Note that AD=28=4⋅7. Then triangle △ADQ must be a multiple of 3− 4−5 (with multiplier 7) or a multiple of 7−24−25 (with multiplier 4). But the latter option implies DQ=4⋅24>30, so the first option is correct. This gives AQ=5⋅7=35.\
Because DQ=3⋅7=21, it follows that QC=30−21=9. Thus triangle △QCP is also a multiple of 3−4−5 (with multiplier 3). This gives PC=4⋅3=12 and PQ=5⋅3=15.\
Finally, because PC=12, it follows that PB=BC−PC=28−12=16. Then triangle △ABQ must be a multiple of 8−15−17 (with multiplier 2), so AP=17⋅2=34. The perimeter of △APQ is 34+15+35=(A)84​.
The problems on this page are the property of the MAA's American Mathematics Competitions