Problem:
The closed curve in the figure is made up of congruent circular arcs each of length , where each of the centers of the corresponding circles is among the vertices of a regular hexagon of side . What is the area enclosed by the curve?
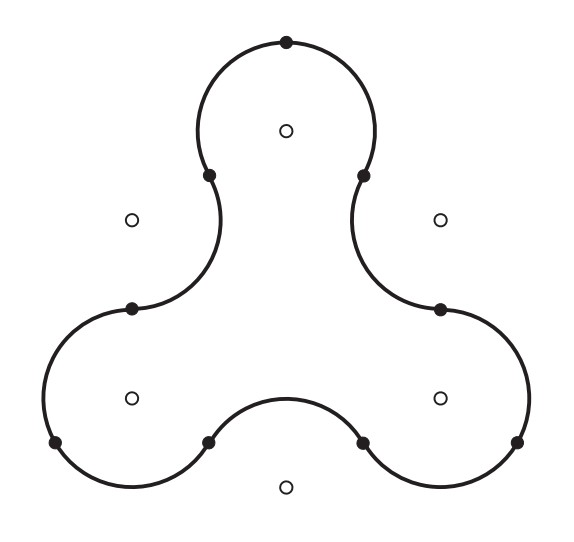
Answer Choices:
A.
B.
C.
D.
E.
Solution:
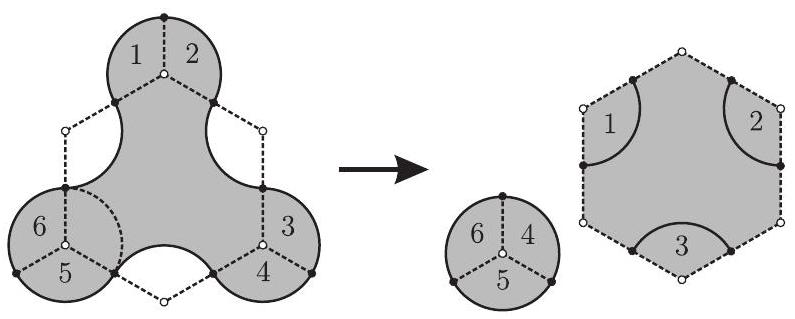
The labeled circular sectors in the figure each have the same area because they are all -sectors of a circle of radius . Therefore the area enclosed by the curve is equal to the area of a circle of radius plus the area of a regular hexagon of side . Because the regular hexagon can be partitioned into congruent equilateral triangles of side , it follows that the required area is
The problems on this page are the property of the MAA's American Mathematics Competitions