Problem:
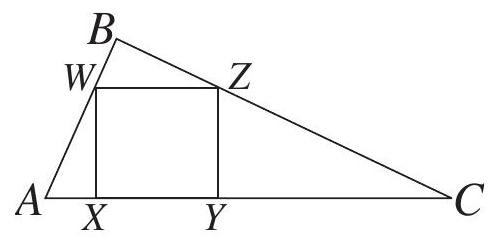
Right â–³ABC has AB=3,BC=4, and AC=5. Square XYZW is inscribed in â–³ABC with X and Y on AC,W on AB, and Z on BC. What is the side length of the square?
Answer Choices:
A. 23​
B. 3760​
C. 712​
D. 1323​
E. 2
Solution:
Let s be the side length of the square, and let h be the length of the altitude of â–³ABC from B. Because â–³ABC and â–³WBZ are similar, it follows that
sh−s​=ACh​=5h​, so s=5+h5h​
Because h=3â‹…4/5=12/5, the side length of the square is
s=5+12/55(12/5)​=3760​
OR
Because â–³WBZ is similar to â–³ABC, we have
BZ=54​s and CZ=4−54​s
Because â–³ZYC is similar to â–³ABC, we have
4−(4/5)ss​=53​
Thus
5s=12−512​s and s=(B)3760​​
The problems on this page are the property of the MAA's American Mathematics Competitions
