Problem:
A quadrilateral has all integer side lengths, a perimeter of , and one side of length . What is the greatest possible length of one side of this quadrilateral?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
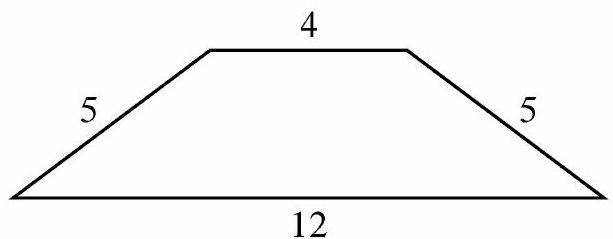
The longest side must have length less than the sum of the other three side lengths. Because the sum of all the side lengths is 26 , this implies that the longest side length must be less than 13 , and because all the side lengths are positive integers, it must be less than or equal to 12 . Such a quadrilateral could have side lengths , and 5 , for example, as shown in the figure.
The problems on this page are the property of the MAA's American Mathematics Competitions