Problem:
For how many ordered pairs (b,c) of positive integers does neither x2+bx+c=0 nor x2+cx+b=0 have two distinct real solutions?
Answer Choices:
A. 4
B. 6
C. 8
D. 12
E. 16
Solution:
The equation x2+bx+c=0 fails to have two distinct real solutions precisely when b2−4c≤0. Similarly the equation x2+cx+b=0 fails to have two distinct real solutions precisely when c2−4b≤0. Hence the given condition is satisfied if and only if b2≤4c and c2≤4b, which can be written as b4≤16c2≤64b. Because b>0, the inequality b4≤64b implies that 1≤b≤4. If b=1, then 1≤16c2≤64, so c=1 or c=2. If b=2, then 16≤16c2≤128, so c=1 or c=2. If b=3, then 81≤16c2≤192, so c=3. If b=4, then 256≤16c2≤256, so c=4. The total number of ordered pairs (b,c) is 2+2+1+1=(B)6.
OR
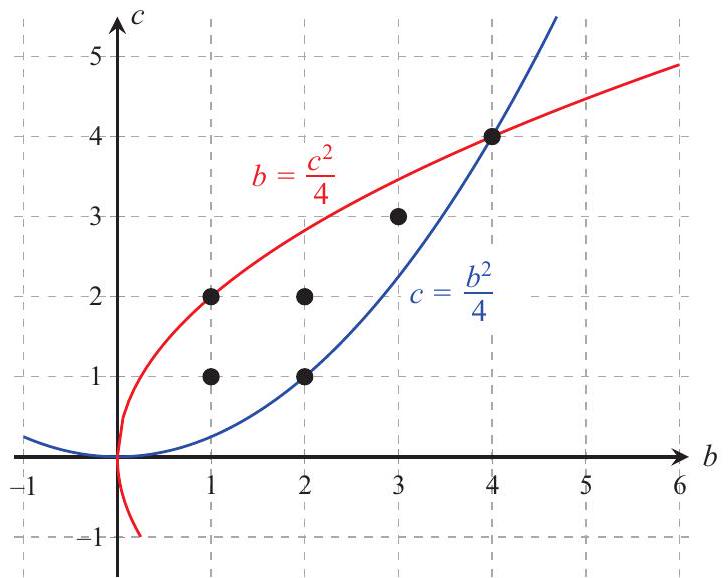
As above, the required ordered pairs must satisfy b2≤4c and c2≤4b, so they are on or inside both of the parabolas c=4b2 and b=4c2 in the bc-coordinate plane. Those parabolas intersect at (0,0) and (4,4), and the lattice points with positive coordinates on or inside both parabolas are (1,1),(1,2),(2,1),(2,2),(3,3), and (4,4), so the number of ordered pairs is (B)6 .
The problems on this page are the property of the MAA's American Mathematics Competitions