Problem:
A regular hexagon has side length . Congruent arcs with radius are drawn with the center at each of the vertices, creating circular sectors as shown. The region inside the hexagon but outside the sectors is shaded as shown. What is the area of the shaded region?
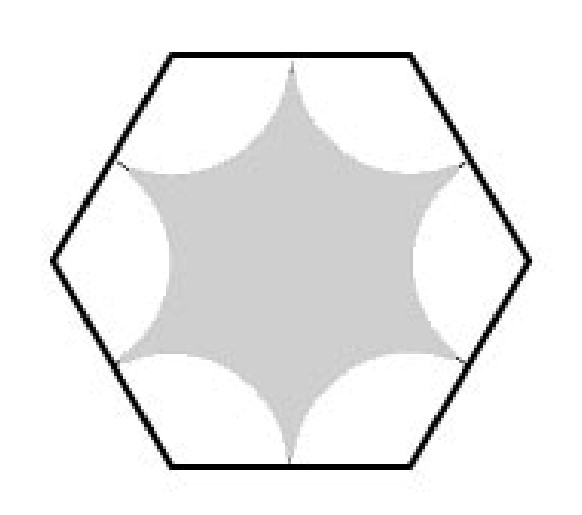
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Each of the sectors has radius and central angle . Their combined area is . The hexagon can be partitioned into equilateral triangles each having side length , so the hexagon has area . The shaded region has area .
The problems on this page are the property of the MAA's American Mathematics Competitions