Problem:
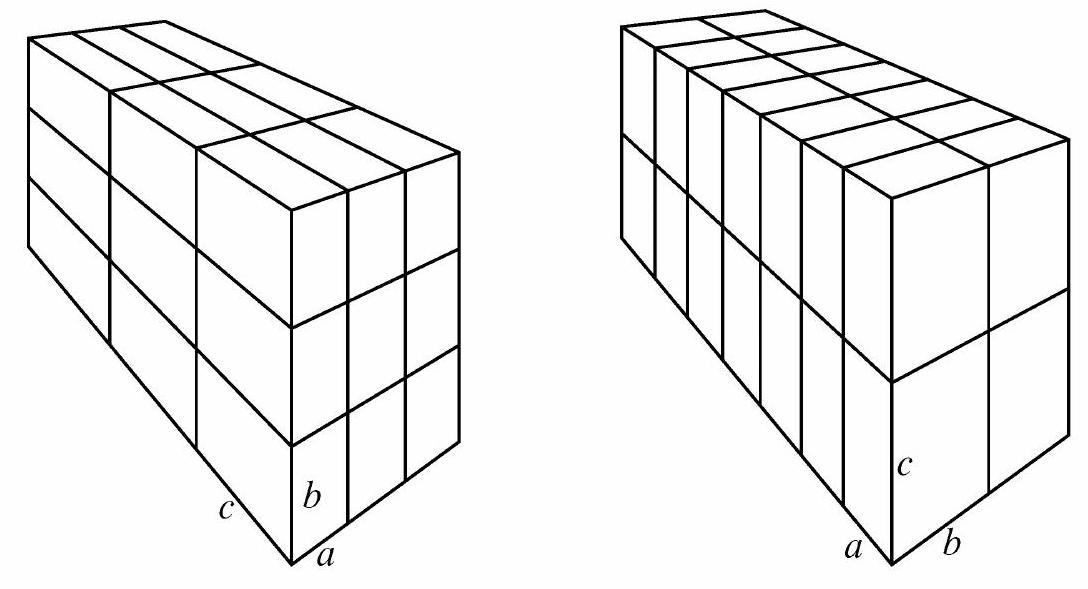
Each of 27 bricks (right rectangular prisms) has dimensions , where , and are pairwise relatively prime positive integers. These bricks are arranged to form a block, as shown on the left below. A 28th brick with the same dimensions is introduced, and these bricks are reconfigured into a block, shown on the right. The new block is 1 unit taller, 1 unit wider, and 1 unit deeper than the old one. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Without loss of generality, assume . Comparing the figures and considering the change in orientation gives rise to the equations , and . To solve this system of linear equations, use the first two equations to write and in terms of , namely and . Substituting these into the third equation gives . Multiplying both sides by 6 yields , which shows that . Back substituting then gives and . The requested sum is .
Note: This problem was inspired by a lovely puzzle created by Thomas O'Beirn called "Melting Block".
The problems on this page are the property of the MAA's American Mathematics Competitions