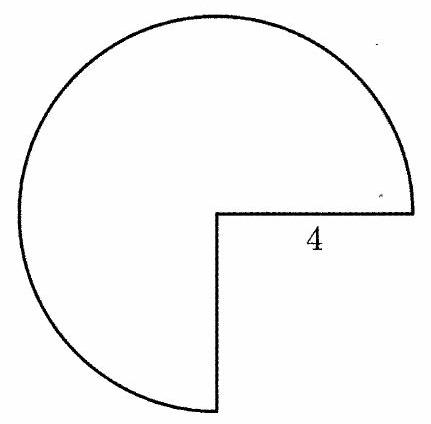
Problem:
A three-quarter sector of a circle of radius inches together with its interior can be rolled up to form the lateral surface of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubic inches?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Notice that when the cone is created, the shown radii when merged will become the slant height of the cone and the intact circumference of the circle will become the circumference of the base of the cone.
We can calculate that the intact circumference of the circle is
Since that is also equal to the circumference of the cone, the radius of the cone is . We also have that the slant height of the cone is . Therefore, we use the Pythagorean Theorem to calculate that the height of the cone is
The volume of the cone is
Using a ruler, measure a circle of radius and cut out the circle and then the quarter missing. Then, fold it into a cone and measure the diameter to be . You can form a right triangle with sides , and then through the Pythagorean theorem the height is found to be
The volume of a cone is . Plugging in we find:
The problems on this page are the property of the MAA's American Mathematics Competitions