Problem:
A round table has radius . Six rectangular place mats are placed on the table. Each place mat has width and length as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length . Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is ?
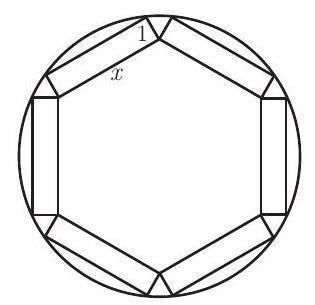
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Select one of the mats. Let and be the two corners of the mat that are on the edge of the table, and let be the point on the edge of the table that is diametrically opposite as shown. Then is also a corner of a mat and is a right triangle with hypotenuse . Let be the inner corner of the chosen mat that lies on the analogous point on the mat with corner , and the corner common to the other mat with corner and the other mat with
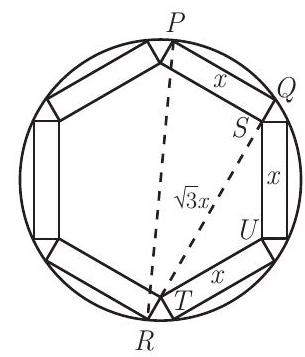
corner . Then is an isosceles triangle with two sides of length and vertex angle . It follows that , so . Apply the Pythagorean Theorem to to obtain , from which . Solve for and ignore the negative root to obtain
The problems on this page are the property of the MAA's American Mathematics Competitions