Problem:
A rhombic dodecahedron is a convex polyhedron where each of the faces is a rhombus, and all of the faces are congruent to each other. The number of edges that meet at a vertex is either , depending on the vertex. What is the number of vertices at which exactly edges meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let , and denote the number of vertices, edges, and faces of the rhombic dodecahedron, respectively. Thus . Each face has 4 edges, and each edge belongs to exactly 2 faces, so . Euler's Formula, , gives . Let denote the number of vertices at which 3 edges meet, and let the number of vertices at which 4 edges meet. Thus . The quantity counts each edge twice, once for each of its endpoints, so . Solving this system of equations yields and .
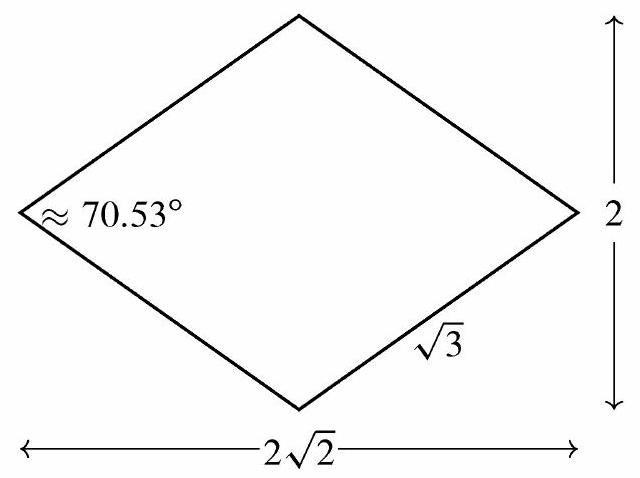
Note: In order to form a rhombic dodecahedron, it is necessary that each rhombus has the dimensions shown below.
The problems on this page are the property of the MAA's American Mathematics Competitions