Problem:
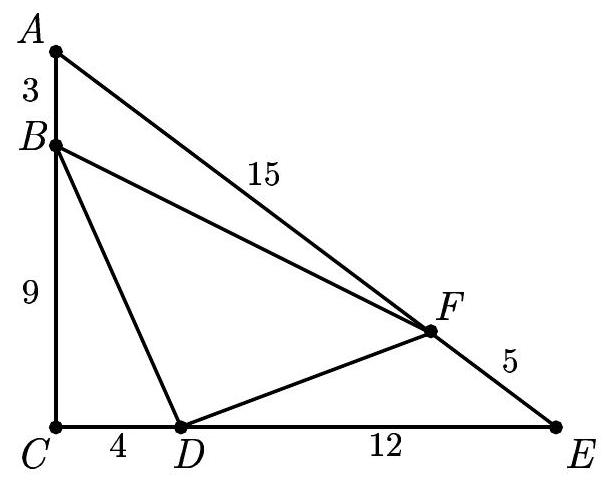
In right triangle â–³ACE, we have AC=12,CE=16, and EA=20. Points B,D, and F are located on AC,CE, and EA, respectively, so that AB=3, CD=4, and EF=5. What is the ratio of the area of â–³BDF to that of â–³ACE?
Answer Choices:
A. 41​
B. 259​
C. 83​
D. 2511​
E. 167​
Solution:
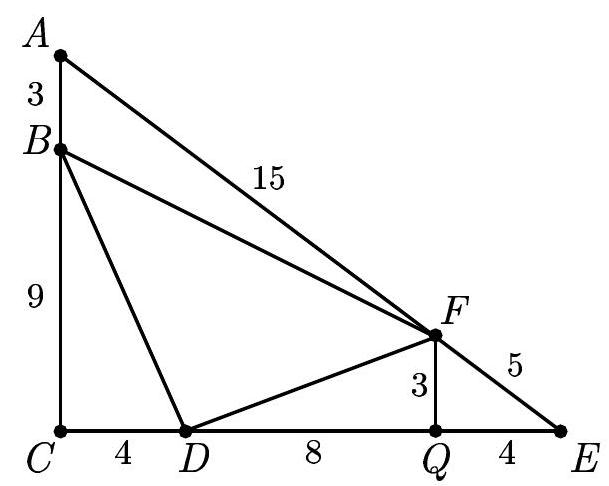
The area of △ACE is (1/2)(12)(16)=96. Draw FQ​⊥CE. By similar triangles, FQ=3 and QE=4. The area of trapezoid BCQF is (1/2)(3+ 9)(12)=72. Since △BCD and △FDQ have areas 18 and 12, respectively, the area of △BDF is 72−18−12=42. The desired ratio is 42/96=(E)7/16​.
OR
Note that each of â–³ABF,â–³BCD, and â–³DEF has a base-altitude pair where the base and altitude are, respectively, 3/4 and 1/4 that of a corresponding base and altitude for â–³ACE. Hence
Area of △ACE Area of △BDF​=1−3(1/4)(3/4)=7/16
Answer: E​.
The problems on this page are the property of the MAA's American Mathematics Competitions
