Problem:
As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region-inside the hexagon but outside all of the semicircles?
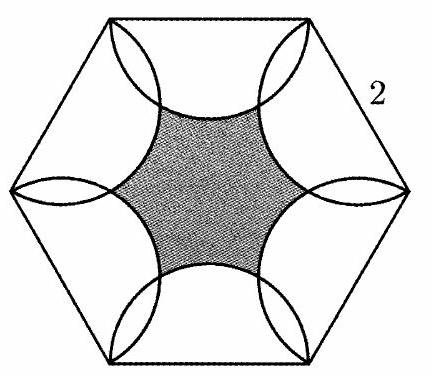
Answer Choices:
A.
B.
C.
D.
E.
Solution:
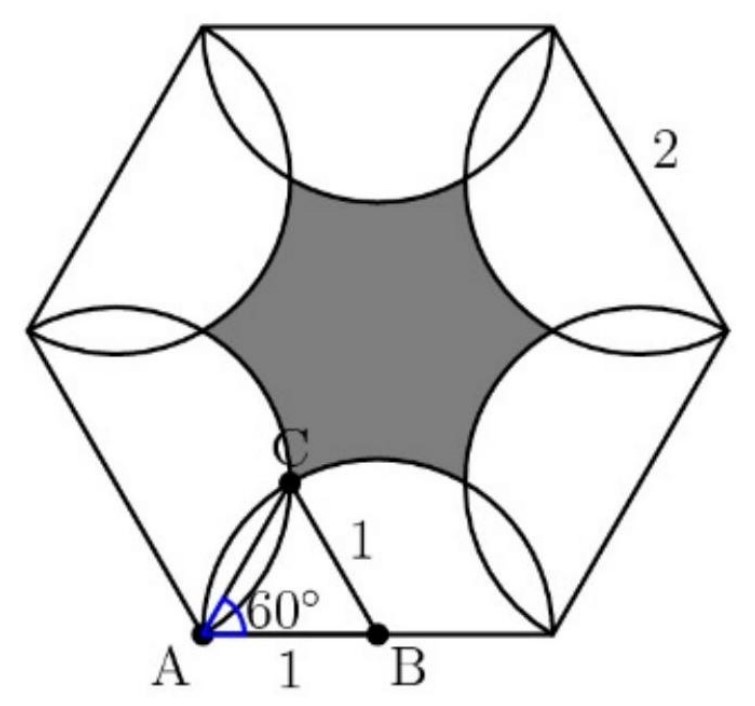
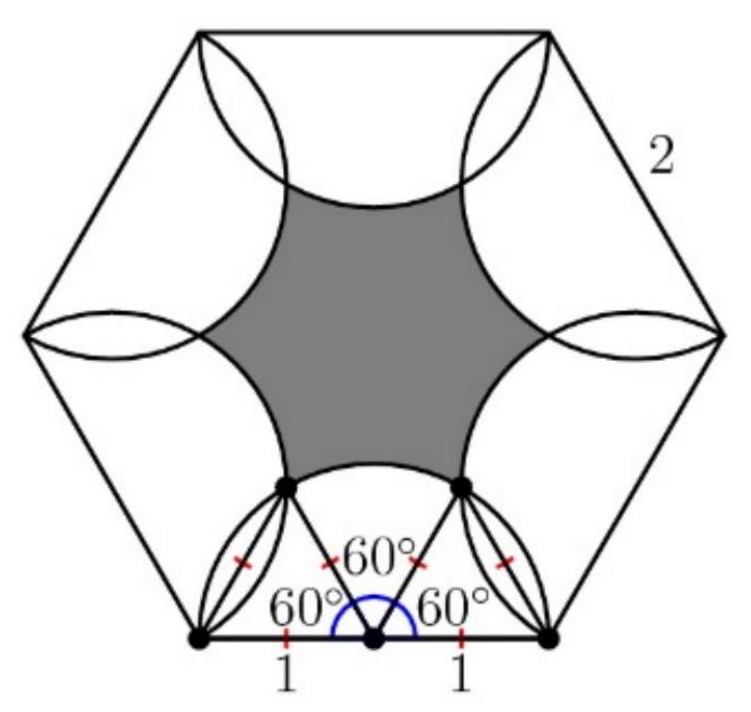
Let point be a vertex of the regular hexagon, let point be the midpoint of the line connecting point and a neighboring vertex, and let point be the second intersection of the two semicircles that pass through point . Then, , since is the center of the semicircle with radius that lies on, , since is the center of the semicircle with radius that lies on, and , as a regular hexagon has angles of , and is half of any angle in this hexagon. Now, using the Law of Sines,
so . Since the angles in a triangle sum to is also . Therefore, is an equilateral triangle with side lengths of .
Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagon is
Since the area of an equilateral triangle can be found with the formula , where is the side length of the equilateral triangle, the area of an equilateral triangle with side lengths of is
Since the area of a circle can be found with the formula , the area of a sixth of a circle with radius is
In each sixth of the hexagon, there are two equilateral triangles colored white, each with an area of , and one-sixth of a circle with radius colored white, with an area of . The rest of the sixth is colored gray. Therefore:
the total area that is colored white in each sixth of the hexagon is , which equals , and
the total area colored white is , which equals .
Since the area colored gray equals the total area of the hexagon minus the area colored white, the area colored gray is
First, subdivide the hexagon into equilateral triangles with side length :
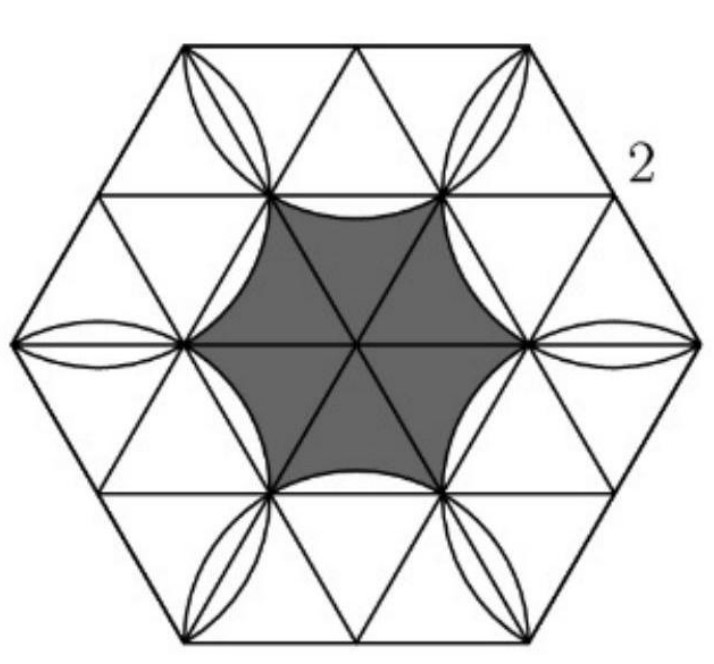
Now note that the entire shaded region is just times this part:
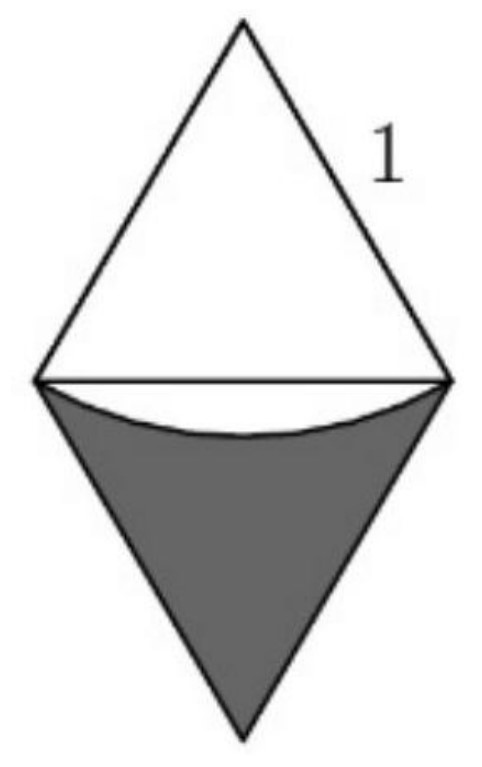
The entire rhombus is just equilateral triangles with side lengths of , so it has an area of:
The arc that is not included has an area of:
Hence, the area of the shaded region in that section is
For a final area of:
The problems on this page are the property of the MAA's American Mathematics Competitions