Problem:
Each of the 12 edges of a cube is labeled 0 or 1 . Two labelings are considered different even if one can be obtained from the other by a sequence of one or more rotations and/or reflections. For how many such labelings is the sum of the labels on the edges of each of the 6 faces of the cube equal to 2 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First suppose that the three edges that share one particular vertex are all labeled 1. Then the rest of the labels are forced by the sum condition, and the figure below is obtained, up to rotation, where those first three edge labels are shown in bold italic font. Note that in this case there is a pair of vertices at the end of an interior diagonal, all of whose edges connected to it are labeled 1 , with the remaining edges all labeled 0 , no three of which mutually share a vertex. Because there are 4 interior diagonals, this gives possible labelings. By symmetry there are another 4 possible labelings in which the roles of 0 and 1 are interchanged.
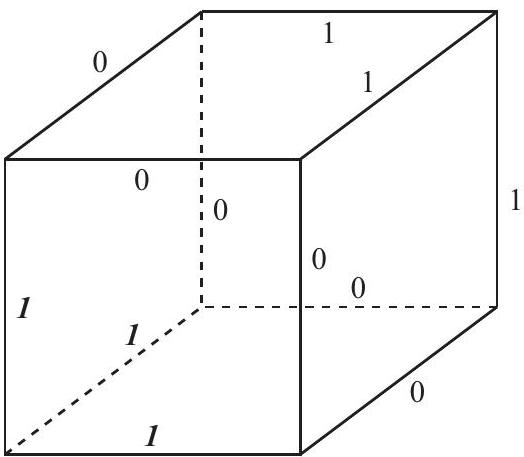
Otherwise, every vertex is connected to two edges labeled 1 and one edge labeled 0 or vice versa. Suppose that the labels of the edges on the bottom face of the cube are in that order. There are 2 possibilities, depending on which label is given to the front bottom edge. There are also 2 possibilities for the label of the left front edge. Once those five labels are determined, the rest of the labels are forced by the sum condition and the fact that no vertex is connected to edges with all the same label. See the figure below, in which the five mentioned labels are shown in bold italic font. This gives labelings.
.jpg)
In the remaining case, the bottom face has labels in that order, which is 4 more cases. Say that the front and left bottom edges are labeled 0 . Then the right front vertical edge can have either label, and once that label is chosen, again the rest of the labeling is forced. See the figure below, in which the five mentioned labels are again shown in bold italic font. This gives more labelings.
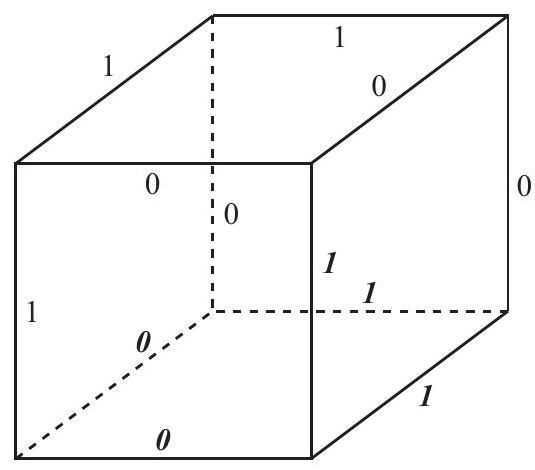
Thus in all there are labelings satisfying the condition.
The problems on this page are the property of the MAA's American Mathematics Competitions