Problem:
In the rectangular parallelepiped shown, AB=3,BC=1, and CG=2. Point M is the midpoint of FG. What is the volume of the rectangular pyramid with base BCHE and apex M?
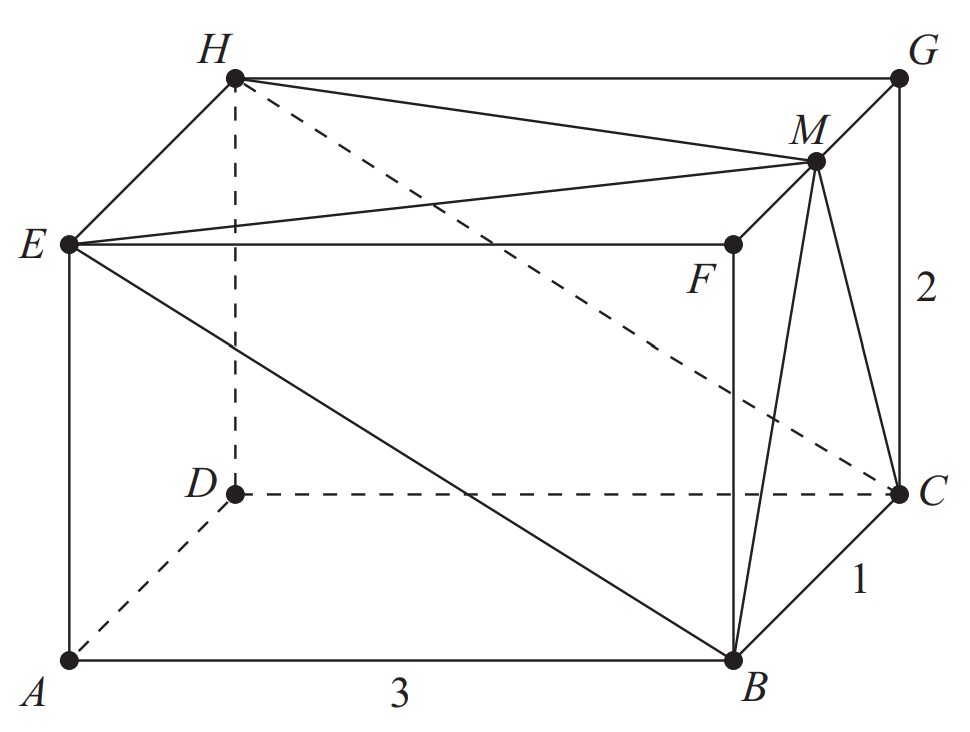
Answer Choices:
A. 1
B. 34​
C. 23​
D. 35​
E. 2
Solution:
The volume of the rectangular pyramid with base BCHE and apex M equals the volume of the given rectangular parallelepiped, which is 6, minus the combined volume of triangular prism AEHDCB, tetrahedron BEFM, and tetrahedron CGHM. Tetrahedra BEFM and CGHM each have three right angles at F and G, respectively, and the edges of the tetrahedra emanating from F and G have lengths 2,3, and 21​, so the volume of each of these tetrahedra
is 61​⋅(2⋅3⋅21​)=21​. The volume of the triangluar prism AEHDCB is 3 because it is half the volume of the rectangular parallelepiped. Therefore the requested volume is 6−3−21​−21​=(E)2​.
OR
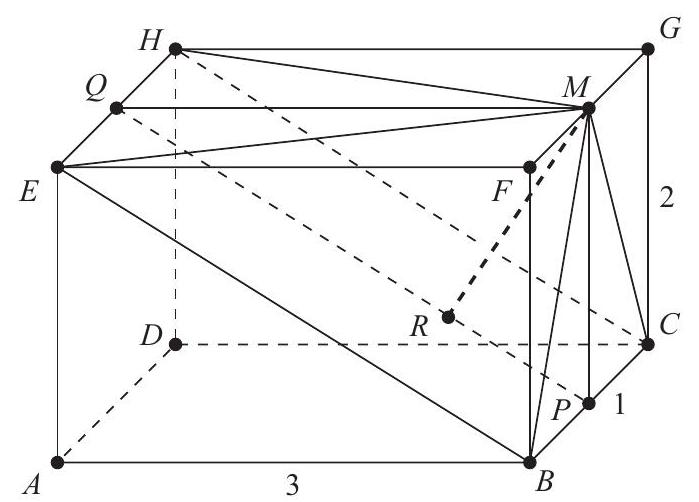
Let P and Q be the midpoints of BC and EH, respectively. By the Pythagorean Theorem PQ=13​. Let R be the foot of the perpendicular from M to PQ​. Then △PMQ∼△PRM, so
13​3​=PQMQ​=PMRM​=2RM​ and RM=13​6​
The requested volume of the pyramid is 31​ times the area of the base times the height, which is
