Problem:
A pyramid has a square base with sides of length and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the apex of the pyramid, and let the base be the square . Then and , so is an isosceles right triangle. Let the cube have edge length . The intersection of the cube with the plane of is a rectangle with height and width . It follows that , from which .
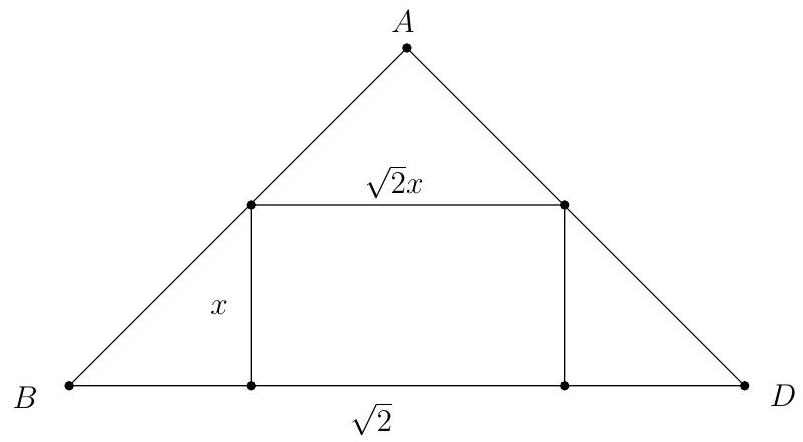
Hence the cube has volume
Let be the apex of the pyramid, let be the center of the base, let be the midpoint of one base edge, and let the cube intersect at . Let a coordinate plane intersect the pyramid so that is the origin, on the positive -axis, and . Segment is an altitude of a lateral side of the pyramid, so , and it follows that . Thus the equation of line is . If the side length of the cube is , then , so . Solving gives , and the result follows that in the first solution.
The problems on this page are the property of the MAA's American Mathematics Competitions